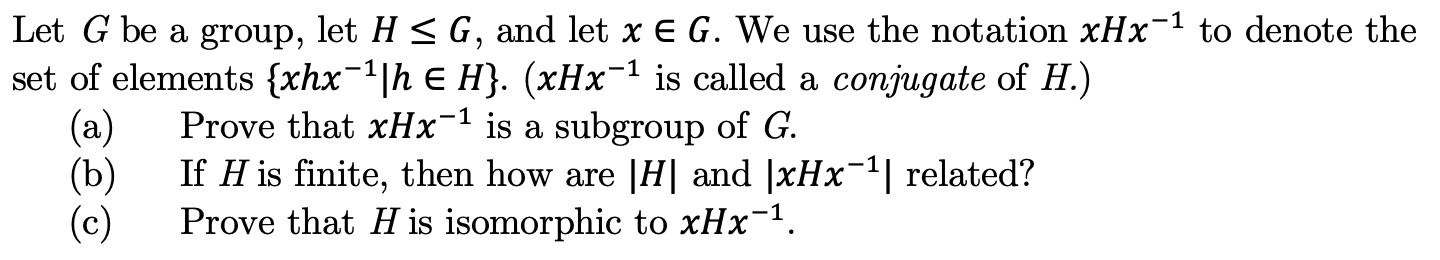
Let G be a group, let H < G, and let x E G. We use the notation xHx1 to denote the set of elements {xhx1h E H}. (xHx is called a conjugate of H.) Prove that xHx-1 is a subgroup of G (a) If H is finite, then how are |H| and |xHx (b) (c) related? Prove that H is isomorphic to xHx1

Let (G, 0) be a group and x € G. Suppose H is a subgroup of G that contains x. Which of the following must H also contain? All elements x y for y E G All "powers" xx, xx0x,... The identity elemente of G Ox*, the inverse of x Enter the smallest subgroup of Z₁5* containing the element [8]15, as a set. Write each congruence class in the form [b]15 where 0 sb<15. You don't have to type out the brackets and subscript"; "15".

Let G be a finite group, i.e., |G| < o∞. (1). Let |G| = 360. Let a e G and |a| = 60. Find the number of left cosets of the subgroup (a²) of G in G (2). Let K be a proper subgroup of H and let H be a proper subgroup of G, i.e., K

Prove that H= { |ne Z} is a subgroup of GL2(R) under multiplication.