
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
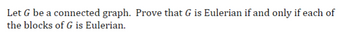
Transcribed Image Text:**Eulerian Graphs and Blocks**
Let \( G \) be a connected graph. Prove that \( G \) is Eulerian if and only if each of the blocks of \( G \) is Eulerian.
In this context, an *Eulerian graph* is a graph containing a closed trail that visits every edge of the graph exactly once. A *block* in a graph is a maximal connected subgraph that has no cut-vertex, which means it is connected and remains connected if any single vertex is removed.
To prove this statement, one needs to show both directions:
- If \( G \) is Eulerian, then each block of \( G \) is Eulerian.
- If each block of \( G \) is Eulerian, then \( G \) is Eulerian.
This involves examining the properties of Eulerian graphs, degree conditions, and the structure of blocks within the graph \( G \).
SAVE
AI-Generated Solution
info
AI-generated content may present inaccurate or offensive content that does not represent bartleby’s views.
Unlock instant AI solutions
Tap the button
to generate a solution
to generate a solution
Click the button to generate
a solution
a solution
Knowledge Booster
Similar questions
- Prove that every graph G on {1,...n} which is acyclic and has n – 2 edges has exactly 2 connected components.arrow_forwardProve: “The complement of the graph G is an Eulerian graph whenever G is also an Eulerian graph of odd order and the complement of G is connected.” Give afigure and details to validate the proof.arrow_forwardLet G be a simple graph. Show that the relation R on the set of vertices of G such that uru if and only if there is an edge associated to {u, v} is a symmetric, irreflexive relation on G.arrow_forward
- Prove that two cycles (a1,a2,...ak), (b1,b2,...bm) are disjoint cycles.arrow_forwardLet G be a graph. Prove that if G has a closed walk of odd length, that the vertices and edges of the walk contain a cycle.arrow_forward(Discrete Math-Graph Theory) Let G=(V,E₁∪E₂∪E₃) be a simple graph such that G₁=(V,E₁) is planar, G₂=(V,E₂) is a forest, and G₃=(V,E₃) is a matching. Prove G is 9-colourable, i.e. its chromatic number satisfies χ(G)≤9.arrow_forward
- Can someone provide the proof for this? TIAarrow_forwardConsider an undirected graph G = (V, E). An independent set is a subset I CV such that for any vertices i, j e I, there is no edge between i and j in E. A set i is a maximal independent set if no additional vertices of V can be added to I without violating its independence. Note, however, that a maximal independent sent is not necessarily the largest independent set in G. Let a(G) denote the size of the largest maximal independent set in G.arrow_forwardThe symmetric difference graph of two graphs G. (V. E.) and G₂ (V₁ E₂) on the same vertex Set is defined as G₁ AG₂:= (V, E, DE₂). E₁ DE ₂ = (E₁ \ E₂) U (E₂\E.) : E₁ E₂ = €₁ 0 € ₂ If G₁ and 6₂ are euleran, show that every Vertex in G, D G₂ has even degree FACT: Each vertex of a evlenan graph has even degree. SO: Show G₁ D G₂ is eulerian.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

