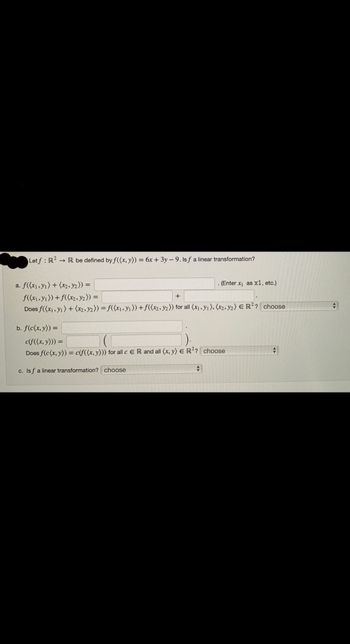
Let f: R2 R be defined by f((x, y)) = 6x+3y-9. lsf a linear transformation? a. f((x1, y1) + (x2, y2)) = (Enter x₁ as x1, etc.) f((x₁, y1)) + f((x₂, y₂)) = + Does f((x1, y1) + (x2, y2)) = f((x₁, y₁)) + f((x2, y2)) for all (x₁, y₁), (x2, y₂) E R2²? choose b. f(c(x, y)) = c(f((x, y))) = Does f(c(x, y)) = c(f((x, y))) for all c ER and all (x, y) E R²? choose c. Isf a linear transformation? choose

Let f: R²R be defined by f((x, y)) = 8y - 4x + 1. Is ƒ a linear transformation? a. f((x1, y₁) + (x2, Y2)) (Enter x₁ as x1, etc.) f((x₁, y₁)) + f((x2, y₂)) = + Does f((x1, y₁) + (x2, 2)) = f((x₁, y₁)) + f((x2, ₂)) for all (x1, y₁), (x2, Y₂) € R²? choose b. f(c(x, y)) = c(f((x, y))) = Does f(c(x, y)) = c(f((x, y))) for all CER and all (x, y) = R²? choose c. Is f a linear transformation? choose

Letf: R2 → R be defined by f((x, y)) = 7x + 7y + 1. Isf a linear transformation? a. f((x₁, y₁) + (x₂, y₂)) = b. f(c(x, y)) = f((x₁, y₁)) + f((x2, y₂)) = + Does f((x₁, y1) + (x₂, y₂)) = f((x₁, y₁)) + f((x2, y2)) for all (x₁, y₁), (x2, y2) ER2? choose . (Enter x₁ as x1, etc.) c(f((x, y))) = Does f(c(x, y)) = c(f((x, y))) for all c ER and all (x, y) = R²? choose c. Is f a linear transformation? choose Note: In order to get credit for this problem all answers must be correct. →

Letf: R² → R be defined by f((x, y)) = -6x - 8y. Isf a linear transformation? a. f((x₁, y₁) + (x2, y₂)) = b. f(c(x, y)) = f((x₁, y₁)) + f((x₂, y₂)) = + Does f(x,y1) + (x₂, y2)) =f((x₁, y₁)) + f((x2, y2)) for all (x₁, y₁), (x₂, y2) E R²? choose (Enter x₁ as x1, etc.) c(f((x, y))) = Does f(c(x, y)) = c(f((x, y))) for all c ER and all (x, y) E R²? choose c. Isf a linear transformation? choose + + +