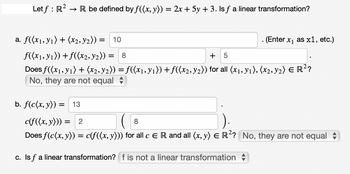
Let ƒ : R² → R be defined by ƒ((x, y)) = 2x + 5y + 3. Is ƒ a linear transformation? a. f((x1, y₁) + (x2, y₂)) = 10 f((x₁, y₁)) +ƒ((x2, Y2)) = . (Enter x₁ as x1, etc.) = 8 + 5 Does f((x₁, y₁) + (x2, y2)) = f((x1, y₁)) +ƒ((x2, y2)) for all (x₁, y₁), (x2, y2) E R²? No, they are not equal b. f(c(x, y)) = 13 c(f((x, y))) = 2 8 Does ƒ(c(x, y)) = c(fƒ((x, y))) for all c E R and all (x, y) = R²? No, they are not equal c. Is ƒ a linear transformation? f is not a linear transformation

- Let ƒ : R² → R be defined by f((x, y)) = 3x + 8y − 1. Is ƒ a linear transformation? a. f((x₁, y₁) + (x₂, y₂)) = f((x₁, y₁)) + f((x2, y₂)) = = + Does ƒ((x₁, y₁) + (x2, y2)) = f((x₁, y₁ )) + ƒ((x2, y2)) for all (x1, Y1 ), (x2, Y2 ) E R² ? choose b. f(c(x, y)) : = c(f((x, y))) = Does f(c(x, y)) = c(f((x, y))) for all c E R and all (x, y) = R²? choose c. Is f a linear transformation? choose . (Enter x₁ as x1, etc.)

Letf: R2 → R be defined by f((x, y)) = 7x + 7y + 1. Isf a linear transformation? a. f((x₁, y₁) + (x₂, y₂)) = b. f(c(x, y)) = f((x₁, y₁)) + f((x2, y₂)) = + Does f((x₁, y1) + (x₂, y₂)) = f((x₁, y₁)) + f((x2, y2)) for all (x₁, y₁), (x2, y2) ER2? choose . (Enter x₁ as x1, etc.) c(f((x, y))) = Does f(c(x, y)) = c(f((x, y))) for all c ER and all (x, y) = R²? choose c. Is f a linear transformation? choose Note: In order to get credit for this problem all answers must be correct. →

Let T: R2→ P2 be a linear transformation for which TH=1-2x and 7[]-=x+ 2x? Find