Explain with full steps please Let E = R be a Euclidean space equiped with the dot product, i.e., for allI2and =in R, we have43u, v) = uU:= Ty1 + 122 + 33- Let ui =andUz =1- Show that B = (u1, u2, u3) is linearly independent set in R.2- Show that B = (u1, u2, u3) is a spanning set of R.3- Deduce that B is a basis of R.%3D4- By using the Gramm-Schmnidt procedure determine an orthonormal basisB, from B.

Answered: Let E R be a Euclidean space equiped…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Question

Explain with full steps please

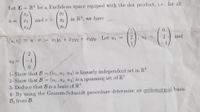
Let E = R be a Euclidean space equiped with the dot product, i.e., for all
I2
and =
in R, we have
43
u, v) = uU:= Ty1 + 122 + 33- Let ui =
and
Uz =
1- Show that B = (u1, u2, u3) is linearly independent set in R.
2- Show that B = (u1, u2, u3) is a spanning set of R.
3- Deduce that B is a basis of R.
%3D
4- By using the Gramm-Schmnidt procedure determine an orthonormal basis
B, from B.

Expert Solution

Step 1

As per our guidelines, we are supposed to answer three sub-parts only. Kindly repost other part as next question.

We will use the following definitions.

1. A set S =(u1, u2, u3,.......un) is linearly independent if the vector equation a1 u1 + a2 u2+........+an un =0 has only trivial solution , i.e. a1, a2 ,............... ...., an=0.

2. If every vector in a vector space can be written as linear combination of u1, u2 , ......, un , then we say the set containing these vectors , say S =(u1, u2, ........., un) is a spanning set of the vector space.