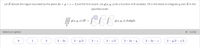
Let E denote the region bounded by the plane 2x + y+ z= 2 and the first octant. Let g(x, y, z) be a function of 3 variables. Fill in the blank to integrate g over E in the specified order: g(x, y, z) dV = g(x, Y, z) dzdydæ E Select an option X CLOSE 1 2 – 2x 2 – y/2 2 – z 2 - z/2 2 – 2x – y 2 – 2x – z 2 – y/2 – z/2

Q: Solve 3(k−4)=18

Q: (D² + 9)y = 0

Q: How do you solve this equation? x/11=x/12-9

Q: It's just one question the solutions Are ther and I need the answer. ThankYou!

Q: Going Round-Trip with the World's Fastest Land Animal According to the Travel Almanac, the world's…

Q: 1 0 4 3 0 1 -2 8 a. 0 0 What is the final solution?

Q: How about the solution for #5?

Q: How do you solve? x=4y+6 x=3y-1

Q: The mathematical model C = 600α + 30,000 represents for a company the cost in dollars of…

Q: How do I solve the Rooster method in Math?

Q: V3 - 1 V3 +1

Q: V2r – 3 + Va + 5 = 0 V 2r – 3 + Vx + 5 = 0

Q: 3x(e* + 1)² − 6x² e* (ex + 1) (ex + 1)4 0

Q: 3 Find the general solution of i = Ax, where A = -8-

Q: How do you solve this without getting an undefined answer?

Q: 4. Solve the equation 1 0 3 1 1 0 4 2 0 2 -3 2 10 -2 2 3 1 14

Q: 4x² +4x%3D 15

Q: How do I solve 1/2h(b1+b2) if h=3, b1=4, and b2=6?

Q: I need help solving q4 parts d-f

Q: Two lighthouses (A and B) are 25 miles apart on a shoreline that runs West to east (Lighthouse A is…