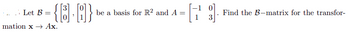
Let \( \mathcal{B} = \left\{ \begin{bmatrix} 3 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix} \right\} \) be a basis for \( \mathbb{R}^2 \) and \( A = \begin{bmatrix} -1 & 0 \\ 1 & 3 \end{bmatrix} \). Find the \( \mathcal{B} \)-matrix for the transformation \( x \to Ax \).

Given that The transformation is

Answered: Let B = {B]. A} mation x→→ Ax. =[%] be…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

-1 0 -4 2 1 1 0 . Let A so that Aa(t) = (t– 1)³. Define T : R³ → R³ by T(x) = Ax. 3 (a) Find a basis B for the generalized eigenspace K1 belonging to A finding a basis for E1 = N(A – 1), extending to a basis for N(A – 11)², and then extending to a basis for K1 = N(A – 1I)³, if necessary. 1 by first (b) Find the matrix [TB of T relative to the basis B and find a matrix P such that P-'AP = [T]B.
Consider B = 2 B' = i) Show that B and B' are bases for R³. [9] ii) Find the coordinate matrices of v = |2| relative to the bases B and B'. iii) Find the transition matrix PB¬B' - iv) Verify that [x(v)]p' = Pg¬p'[x(v)]g- %3D
Exercise 4. (a) Compute the center of GL(2, R). (Hint: use the following test matrices [] and [1] (b) Compute the center of SL(2, R).
In the vector space P of polynomials of 2' degree atmost two, the first column of the matrix of transition from the basis B=(e₁=1+x;e₂=x+x²e₂=3+x²) to basis A={r= 1− 3x; s=x; t=x²} is: A. 1 O*:) B. -2 *(-9 - 1 1 06 (8) D. 0° (:)
2. Let a = 2 ---- X= -2 4 and y = 4 2 (a) Find P, the projection matrix along the span of a. (b) Find proja (x). (c) Find proja (y). 3. Let A be a nonsingular 2 x 2 matrix. (a) Find P, the projection matrix onto C(A). (b) Find C(A) and comment on the result of part (a).
9. Consider the following 2 x 2 matrix A and basis S of R²: A ¹ = [² %) and 5 = {[_¹₂] · [_³;]} The matrix A defines a linear operator on R². Find a matrix B that represents the mapping A relative to the basis S.
Label the following statements as true or false. (a) Suppose that B = {x1,x2, ..., xn} and B' = {x1, x2, ... , x,} are ordered bases for a vector space and Q is the change of coordinate matrix that changes B'-coordinates into 3-coordinates. Then the jth column of Q is [x;]g. (b) Every change of coordinate matrix is invertible. (c) Let T be a linear operator on a finite-dimensional vector space V, let 3 and B' be ordered bases for V, and let Q be the change of coordinate matrix that changes B'-coordinates into 3-coordinates. Then [T] = Q[T]8•Q¬!.
Consider the linear transformation T: R^ →R" whose matrix A relative to the standard basis is given. [³ A = (a) Find the eigenvalues of A. (Enter your answers from smallest to largest.) (1₁, 12) = 4,5 B₂ 3-2 (b) Find a basis for each of the corresponding eigenspaces. B₁ = 1,2 128 1,1 = A' = 1 6 (c) Find the matrix A' for T relative to the basis B', where B' is made up of the basis vectors found in part (b). X 5 5 1 2 ↓ 1
Consider the vector space V of all the real polynomials of degree less than or equal to three, p(x) = ax^3 + b x^2 + c x + d, and consider the linear transformation T: V ------> V given by the derivative, i.e., T( p ) = p' = 3ax^2 + 2 b x + c. Find the eigenvalues and eigenvectors of this transformation.

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS

Let B = {B]. A} mation x→→ Ax. =[%] be a basis for R2 and A = Find the B-matrix for the transfor-