
Elements Of Modern Algebra
8th Edition
ISBN: 9781285463230
Author: Gilbert, Linda, Jimmie
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
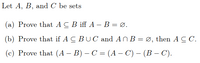
Transcribed Image Text:Let A, B, and C be sets
(a) Prove that A C B iff A – B = Ø.
(b) Prove that if A C BU C and ANB = Ø, then A C C.
(c) Prove that (A – B) – C = (A – C) – (B – C).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Label each of the following statements as either true or false. 2. for all nonempty sets A and B.arrow_forwardExpress (AB)(AB) in terms of unions and intersections that involve A,A,B,andBarrow_forward[Type here] 7. Let be the set of all ordered pairs of integers and . Equality, addition, and multiplication are defined as follows: if and only if and in , Given that is a ring, determine whether is commutative and whether has a unity. Justify your decisions. [Type here]arrow_forward
- Label each of the following statement as either true or false. 9. If ab and ba then a=b.arrow_forwardShow that if ax2+bx+c=0 for all x, then a=b=c=0.arrow_forward6. For the given subsets and of Z, let and determine whether is onto and whether it is one-to-one. Justify all negative answers. a. b.arrow_forward
- For what values of c is c(1,2,3)=1?arrow_forward7. For the given subsets and of Z, let and determine whether is onto and whether it is one-to-one. Justify all negative answers. a. b. c. d.arrow_forward11. (See Exercise 10.) According to Definition 5.29, is defined in by if and only if . Show that if and only if . 10. An ordered field is an ordered integral domain that is also a field. In the quotient field of an ordered integral domain define by . Prove that is a set of positive elements for and hence, that is an ordered field. Definition 5.29 Greater than Let be an ordered integral domain with as the set of positive elements. The relation greater than, denoted by is defined on elements and of by if and only if . The symbol is read “greater than.” Similarly, is read “less than.” We define if and only if. As direct consequences of the definition, we have if and only if and if and only if . The three properties of in definition 5.28 translate at once into the following properties of in . If and then . If and then . For each one and only one of the following statements is true: . The other basic properties of are stated in the next theorem. We prove the first two and leave the proofs of the others as exercises.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning, Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell

Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell