Question
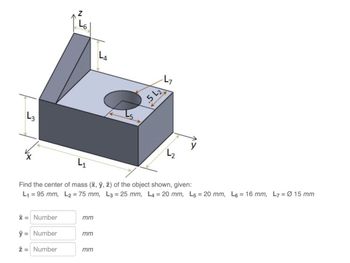
Transcribed Image Text:L3
15
L6
LA
.5 L₂
L7
L₂
y
L₁
Find the center of mass (x, y, z) of the object shown, given:
L₁ = 95 mm, L₂ = 75 mm, L3 = 25 mm, L4 = 20 mm, L5 = 20 mm, L6 = 16 mm, L7 = Ø 15 mm
x = Number
mm
ỹ = Number
mm
z = Number
mm
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Assume that the board you used was covered with two materials, material 1 and material 2. If the height where the wooden block started to slide down is higher on material 2 than on material 1, what can we say about the μs and μk associated with material 2 as compared to material 1? a. μs and μk on material 2 is higher than on material 1b. μs and μk on material 1 is higher than on material 2c. μs on material 2 is higher than on material 1, but μk material 1 is higher than on material 2d. μs on material 1 is higher than on material 2, but μk material 2 is higher than on material 1e. Regarless of any height, μs and μk is same on material 1 and material 2arrow_forwardd and earrow_forwardThe question is whether these relationships are linear or non-linear, can you please inform me on how I'd be able to tell?arrow_forward
- Figure x Part A - Moment due to a force specified by magnitude and endpoints F As shown, a member is fixed at the origin, point O, and has an applied force F, the tension in the rope, applied at the free end, point B. (Figure 1) VE ΑΣΦ ↓↑ vec Mo 0.013,97.9, - 196 Submit The force has magnitude F = 140 N and is directed as shown. The dimensions are x₁ = 0.450 m, x₂ = 1.70 m, y₁ = 2.60 m, and z₁ = 1.30 m. B What is the moment about the origin due to the applied force F? Express the individual components of the Cartesian vector to three significant figures, separated by commas. ► View Available Hint(s) Previous Answers X Incorrect; Try Again; 4 attempts remaining 1 of 3 ? i, j, k] N · marrow_forwardQUESTION 1 The linear mass density (A) of a rod of length L is given by A = a+ Bx2 where a and B are constants and x is the distance from one end. What is the total mass of this rod? a + BL2 aL + (BL³)/ 3 (a+ Bx2)L O al + (BL2)/ 2arrow_forwardI need help on this question the answer for question number one should be 31.93 kg.m^2 and for question 2 it's 1.68m from top and 3 sec.arrow_forward
- The Statue of Liberty in New York City is approximately 305 ft305 ft tall. How many U.S. dimes would be in a stack of the same height? Each dime is 1.35 mm1.35 mm thick. number of dimes: Each dime has a mass of 2.268 g.2.268 g. How much would the stack of dimes from the previous question weigh? mass: g What is the value, in dollars, of the same stack of dimes? value: dollars The 2017 U.S. gross domestic product (GDP) was valued at 19,390,604,000 dollars.19,390,604,000 dollars. How many Statue of Liberty‑height stacks of dimes are needed to match the GDP in value? number of stacks:arrow_forward1. Determine the x, y, and z components of the 900 N force shown in Figure 1. 22 900 N 65° y 20⁰ 35⁰ Figure 1 750 N 25° xarrow_forwardGiven values: m1 = 10kg, r1=75 cm, m3=20kg, r3=25cm, m4=5kg, had to find the value of r4=? I got r4=50cm m1 = 10 kg at r1 = 75cm m3 = 20 kg at r3 = 25cm m4 = 5 kg at r4 = 50cm 1. Compute the theoretical value of r4 using the following equation: r1m1 = r3m3 + r4m4 Substitute the values of r1, r3, m1, m3, m4 and solve for r4 theoretical value and find r4 experimental valuearrow_forward
- 1. The setup shown by the diagram below was used to calculate the force experienced by a small mass m situated at a distance r from the geometric center of a spherical shell with mass M, radius R, and a wall thickness of t. M C dᎾ R 0 Rde A Rsine B r Ф dF Ф m If the mass is situated outside the spherical shell, the force can be calculated by integration from l = (r - R) to l= (r+ R), as shown here: l=r+R R - [ &F="TOmp: +(1+²²=² ) We SdF=fGmpat- de l=r-R What would the limits of integration be if the mass were situated inside the spherical shell? Include a labeled diagram to represent this situation.arrow_forward2. You are manufacturing a can which is a perfect cylinder. The ideal volume of the can is 375 cm3. Since the bases of the cylinders are exactly 50 cm2, the volume of the can is V = 50h where h is the height of the can in centimeters. You need to cut the sides of the can so the volume has at most an error of 10 cm³. Give the range of heights the can could have and still meet the required specifications for its volume.arrow_forward
arrow_back_ios
arrow_forward_ios