
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Justify and explain that if X and Y are independent random variables with respective parameters lambda 1 and lambda 2, calculate the conditional distribution of X given that X+Y=n
Expert Solution
arrow_forward
Step 1
It is provided that X+Y = n and X, Y are non-negative, then X can choose 1, …, n.
Therefore,
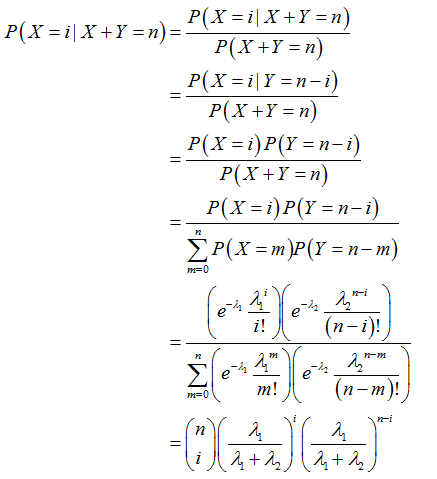
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- Suppose that the time students wait for a bus can be described by a uniform random variable X, where X is between 15 minutes and 55 minutes. (a) What is the probability, P that a student will wait between 15 and 25 minutes for the next bus?P = (b) What is the probability, P that a student will have to wait at least 25 minutes for the next bus?arrow_forwardIt is known that 51% of American college students fail a course during their freshman year. A university journal club randomly samples 9 upperclassmen and asks them if they failed a course during their freshman year, 3 say they have. Suppose a hypothesis test is to be conducted to determine if the proportion of students who failed a course during their freshman year is less than 0.51. The random variable is X = the number of students in the sample that failed a course during their freshman year. What values of X are considered "as or more unusual" than the observed count if the null hypothesis is true? X ≥ 3 3 ≤ X ≤ 4.59 X ≥ 4.59 X ≤ 4.59 X ≤ 3arrow_forwardIt is said that the number of traffic accidents in Sinchon Rotary follows the Poisson distribution, of which the expected value is three times per hour. When the number of traffic accidents in the Sinchon Rotary during the 30 days independent of each other is X1, X2, ..., X30, answer the following questions. (1) The random variable Y is the sum of the number of traffic accidents in the Sinchon Rotary for 30 days independent of each other. Find the distribution of Y. (e.g. normal distribution, binomial distribution, etc.) (2) Use (1) to calculate the probability that the time until two traffic accidents occur in 30 days exceeds 20 hours. (3) For three years, Mike had never seen a traffic accident while traveling the Sinchon Rotary almost every day, so he usually thought that the number of traffic accidents would be less than three per hour. To confirm this, A surveyed the number of traffic accidents at Sinchon Rotary for one hour for 30 days, and as a result, the average number of…arrow_forward
- a manufactoring company produces 10,000 platics cups per day. This company supplies cups to a supermakret which sells them in packs of 10 per pack. Ig less than two of a ranfdomlu slected pack (of 10 cups) from the order are defective, the supermarket accepts the whole order. The proportion of defective cups produced by the manufactoring company is 10%. Let X be the random variable representing the number of defective cups in a pack. i) identify the type of distribution being described in this question and write down the value of its parameters. ii) what is the probability that the order will be accepted? iii) What is the probability that a randomly selected pack (of 10 cups) has more than two defective cups?arrow_forwardSuppose that40%of the applicants for a certain job possess advanced training in computerprogramming. Applicants are interviewed sequntially and are selected at random from the pool. Find theprobability that the 4th applicant with advanced training in programming is found on the 8th interview.To answer this question, first identify the random variable, its distribution and the parameter(s) of the distribution.arrow_forwardAt a toll-booth on-ramp there is a stochastic arrival distribution. Vehicles are counted in 20-second intervals, and vehicle counts are taken in 120 of these time intervals. Based on data collected, no vehicles arrived in 18 of the 120 count intervals. What is the number of the 120 intervals that 3 cars arrived?arrow_forward
- Define Probabilities and Moments of Continuous Random Variables?arrow_forwardAssume that hybridization experiments are conducted with peas having the property that for offspring, there is a 0.75 probability that a pea has green pods. Assume that the offspring peas are randomly selected in groups of 34. Is a result of 2 peas with green pods a result that is significantly low? Why or why not?arrow_forwardSuppose that Wall A is constructed by stacking 30 metal blocks, and that the height of each metal block is an independent N(50, 10) normal random variable. Suppose that Wall B is constructed by stacking 25 wood blocks, and that the height of each wood block is an independent N(61, 4) normal random variable. What are the distributions of the heights of Wall A and Wall B? (b) What is the probability that Wall A is taller than Wall B?arrow_forward
- The executives at a software company called Front Line are trying to decide if they should continue to provide free coffee in their breakrooms. They have 79 employees and each employee has a 67% chance of drinking coffee in the break room each day. Recall, for a binomial random variable, dbinom(j,n,p) P(Y = j) and pbinom(j,n,p) = P(Y < j). What is the expected number of employees who will drink coffee in one day?arrow_forwardFind the expected number of infected ducks in a sample of 5 ducks if the probability of an infected duck is 0.3 and the ducks can be considered independent.arrow_forwardA large ski mountain has a fleet of 4 snowmobiles it uses during the winter season. It believes that the time between consecutive repair operations for a single snowmobile is an exponential random variable with a mean of .75 weeks. There are two dedicated technicians that are capable of repairing the snowmobiles. A broken down snowmobile will be repaired by one of these technicians (when one becomes available) and the repair time of a snowmobile can be modeled as an exponential random variable with a mean of .4 weeks. (a) Describe a queueing system model of the repair operations of the snowmobiles by answering the following questions: What are the customers in the queueing system? What are the servers and what service is being provided? b) Provide the rate transition diagram of the birth and death process that captures the queueing system. Be sure to provide λn and µn for each relevant value of n and your logic behind any calculations used to obtain them (c) Provide the…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
