Answered: It started out as a snowy week - it…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Question

a) using the graph, on what days is the snow on the ground increasing?Decreasing? How do you know from the graph? ( Express in interval notation)

b) set up and evaluate a definite integral that represents the shaded region in the graph.

c) what does the definite integral represent in the context of the problem?

d) if there was 6 inches of snow on the ground to begin, how much snow is there after 4 days?

It started out as a snowy week - it snowed for an entire day! Then it warmed up for a day, snowed for two days straight, and has been dry since. An equation that models the snowfall rate (in inches/day) for the first 5 days is given by the
equations
( cos(2t) 0<ts
S(t) =
3.92. A graph of the snowfall rate is shown below:
4.
Note:
S(1)

Expert Solution

part a

The given graph is shown below.

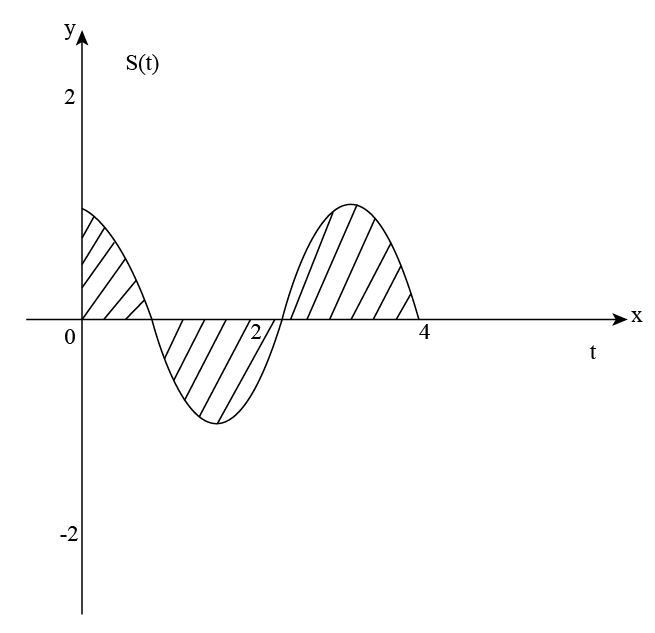
From the graph, it can be seen that in the interval $[0, - \frac{3}{2}], S (t)$ is decreasing , in $[- \frac{3}{2}, 3], S (t)$ is increasing and $[3, 4]$ it is decreasing again. For $t \geq 4, S (t) = 0$ . It implies that between ay 0 and day $\frac{3}{2}$ the snowfall rate is decreasing and from day $\frac{3}{2}$ to day 3, this rate is increasing. From day 3, it is again decreasing and from day 4 and onwards, this rate becomes zero.

part b

The given model representing the snowfall rate is given by

$S (t) = \{\begin{cases} \cos 2 t, 0 \leq t \leq \frac{5 π}{4} \\ 0, t \geq \frac{5 π}{4} \end{cases} \frac{5 π}{4} \approx 3.92$

Hence,

$\begin{array}{rcl} \int_{0}^{4} S (t) d t & = & \int_{0}^{\frac{5 π}{4}} S (t) d t + \int_{\frac{5 π}{4}}^{4} S (t) d t \\ = & \int_{0}^{\frac{5 π}{4}} \cos 2 t d t \\ = & \frac{1}{2} \sin \frac{5 π}{2} \\ = & \frac{1}{2} [a s \sin \frac{5 π}{2} = 1] \end{array}$

Trending now

This is a popular solution!

Step by step

Solved in 4 steps with 1 images

Knowledge Booster

$Definite Integral$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions