
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
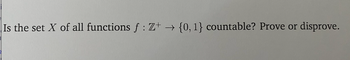
Transcribed Image Text:**Question:**
Is the set \( X \) of all functions \( f : \mathbb{Z}^+ \rightarrow \{0,1\} \) countable? Prove or disprove.
---
To determine if the set \( X \) of all functions from the set of positive integers \( \mathbb{Z}^+ \) to the set \(\{0,1\} \) is countable, we first need to understand some key concepts:
1. **Countable Sets:**
- A set is **countably infinite** if its elements can be placed in one-to-one correspondence with the positive integers \( \mathbb{Z}^+ \) (i.e., it can be listed as \( \{a_1, a_2, a_3, \ldots\} \)).
- A set is **uncountable** if it is not countable (i.e., it cannot be listed in this manner).
2. **Functions:**
- A function \( f : \mathbb{Z}^+ \rightarrow \{0,1\} \) assigns to each positive integer either 0 or 1.
- Each function can be represented as an infinite sequence of 0s and 1s. For example, one such function might look like \( f(1)=0, f(2)=1, f(3)=0, \ldots \), which corresponds to the sequence \( (0, 1, 0, \ldots) \).
3. **Cardinality:**
- The set of all infinite sequences of 0s and 1s has the same cardinality as the power set of the natural numbers \( \mathcal{P}(\mathbb{N}) \).
- The cardinality of \( \mathcal{P}(\mathbb{N}) \) is \( 2^{\aleph_0} \) (read as \( 2 \) raised to the power of \( \aleph_0 \), where \( \aleph_0 \) denotes the cardinality of the set of positive integers \( \mathbb{Z}^+ \), representing the smallest infinity, also known as countable infinity).
**Proof:**
1. Assume \( X \) is countable. Then, there would exist a bijection between the set of all functions \(
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- Determine whether each of these functions f:Z->Z is one-to-one, on-to, one-to-one correspondence, respectively. a) f(n) = n-1 b) fln)= n² +1 c) f(n)= n² d) fir) = [n/2]arrow_forwardSuppose that f:I->R is a continuous function and that |f| is a constant function. Prove that f is a constant functionarrow_forwardLet n be a positive integer and let f : [0..n] → [0..n] be an injective function. Define the function g : [0..n] → Z as g(x) = n - (f(x))². Prove that is also injective.arrow_forward
- Let f: X → Y. Prove that f is one to one if B = f -1(f(B)) for all B ⊆ X.arrow_forwardWhich of the following function f: R X R → R is not onto? 1 2x - 3 2 3x3 - x 3 x2-2x 4 f(x) = x2- 5x + 5arrow_forwardSuppose f is an entire function such that there is a number M such that Re(f(z))² – Im(f(z))² < M for all z. Prove that f must be constant.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

