
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
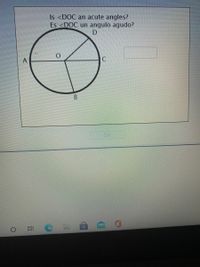
Transcribed Image Text:Title: Understanding Acute Angles in Circles
---
**Question:**
Is ∠DOC an acute angle?
Es ∠DOC un ángulo agudo?
---
**Diagram:**
This diagram features a circle with center \( O \). There are four labeled points on the circle: \( A \), \( B \), \( C \), and \( D \). Lines \( \overline{OA} \), \( \overline{OB} \), \( \overline{OC} \), and \( \overline{OD} \) are radii of the circle, dividing the circle into four segments.
**Explanation:**
- **Point \( O \):** The center of the circle.
- **Points \( A \), \( B \), \( C \), \( and D \):** Points on the circumference of the circle.
- **Radii \( \overline{OA} \), \( \overline{OB} \), \( \overline{OC} \), and \( \overline{OD} \):** These lines are connecting the center \( O \) to the points on the circumference.
**Question Details:**
- The specific angle in question is ∠DOC, formed by the radii \( \overline{OD} \) and \( \overline{OC} \).
- The term "acute angle" refers to an angle that is less than 90 degrees.
**Considerations:**
To decide whether ∠DOC is acute, observe the position of lines \( \overline{OD} \) and \( \overline{OC} \). If the angle formed between them is less than 90 degrees, it is considered acute.
**Answer Box:**
To the right of the question is a blank box where the answer can be input.
**Button:**
Below the diagram and question is an “OK” button to submit the answer.
---
**Educational Notes:**
- An acute angle is always less than 90 degrees.
- A helpful way to visualize this is by comparing the angle to a right angle (which is exactly 90 degrees).
---
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning