
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
Python only.
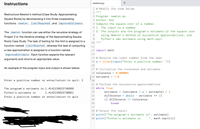
Transcribed Image Text:Instructions
newton.py
1 # Modify the code below
2 II I| ||
Restructure Newton's method (Case Study: Approximating
3 Program: newton.py
Square Roots) by decomposing it into three cooperating
4 Author: Ken
functions: newton , limitReached , and improveEstimate .
5 Compute the square root of a number.
6 1. The input is a number.
7 2. The outputs are the program's estimate of the square root
using Newton's method of successive approximations, and
Python's own estimate using math.sqrt.
The newton function can use either the recursive strategy of
8
Project 2 or the iterative strategy of the Approximating Square
9.
Roots Case Study. The task of testing for the limit is assigned to a
function named limitReached , whereas the task of computing
11
a new approximation is assigned to a function named
12 import math
improveEstimate . Each function expects the relevant
13
arguments and returns an appropriate value.
|14 # Receive the input number from the user
15 x =
float(input("Enter a positive number: "))
16
An example of the program input and output is shown below:
17 # Initialize the tolerance and estimate
18 tolerance = 0.000001
19 estimate = 1.0
Enter a positive number or enter/return to quit: 2
20
21 # Perform the successive approximations
The program's estimate is 1.4142135623746899
22 while True:
estimate = (estimate + x / estimate) / 2
difference
if difference <= tolerance:
23
Python's estimate is
1.4142135623730951
Enter a positive number or enter/return to quit
24
abs (x - estimate ** 2)
25
26
break
27
28 # Output the result
29 print("The program's estimate is", estimate)
30 print("Python's estimate is
', math.sqrt(x))
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education