
Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
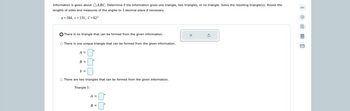
Transcribed Image Text:### Acute Triangle Analysis and Calculation
---
#### Given Data:
Information is provided about triangle \( \Delta ABC \). The task is to determine whether the given information results in one triangle, two triangles, or no triangle. If feasible, solve for the resulting triangle(s) by finding the lengths of the sides and the measures of the angles to one decimal place as necessary.
- \( a = 184 \)
- \( c = 131 \)
- \( C = 62^\circ \)
---
#### Instructions:
1. **Determine Possibility of Triangle Formation**
- Evaluate whether the given dimensions and angle result in:
- No triangle
- One unique triangle
- Two different triangles
2. **Solve for Unknowns**
- If one unique triangle or two triangles are possible, solve for the remaining angles \( A \), \( B \), and the length of side \( b \).
3. **Entry Fields for Solutions**
- No Triangle: Select if no triangle can be formed.
- One Unique Triangle: Enter the angles \( A \) and \( B \), and the length of side \( b \).
- Two Triangles: Enter the angles \( A_1 \), \( B_1 \), and \( A_2 \), \( B_2 \), and the lengths of side \( b_1 \) and \( b_2 \).
#### Selection Options with Inputs:
- **No Triangle**: Select this if based on calculations, the geometrical constraints prevent forming any triangle.
- **One Unique Triangle**:
- Angle \( A \approx \_\_\_\degree \)
- Angle \( B \approx \_\_\_\degree \)
- Side \( b \approx \_\_\_\)
- **Two Triangles**:
- **Triangle 1:**
- Angle \( A \approx \_\_\_\degree \)
- Angle \( B \approx \_\_\_\degree \)
- Side \( b \approx \_\_\_\)
- **Triangle 2:**
- Angle \( A \approx \_\_\_\degree \)
- Angle \( B \approx \_\_\_\degree \)
- Side \( b \approx \_\_\_\)
#### Additional Features:
- Utilize the function buttons to reset or clear the entries:
- **Reset Button**: Clears all fields to default.
- **
![### Transcription of Educational Content
#### Problem Statement:
- There are two triangles that can be formed from the given information.
#### Triangle 1:
- **Angle A**: \( \approx \) [input box] \( ^\circ \)
- **Angle B**: \( \approx \) [input box] \( ^\circ \)
- **Side b**: \( \approx \) [input box]
#### Triangle 2:
- **Angle A**: \( \approx \) [input box] \( ^\circ \)
- **Angle B**: \( \approx \) [input box] \( ^\circ \)
- **Side b**: \( \approx \) [input box]
#### Explanation:
The task is to determine the angles and side length for two possible triangles based on some given information. The angles and sides are denoted by input boxes where values need to be provided. Each triangle's angles (A and B) and one side (b) need to be estimated.
The diagrams are absent, but the layout suggests boxes to fill in the answers for the angles (in degrees) and the side length.
### Analytical Steps:
1. **Enter the approximate values for angles A and B, ensuring they sum up to less than \(180^\circ\).**
2. **Input the lengths of side b for both triangles.**
3. **Verify that the triangles formed are valid and adhere to the triangle inequality theorem.**
This layout is useful in understanding the ambiguity in forming triangles given partial data and teaches the application of angle and side relations in geometry.](https://content.bartleby.com/qna-images/question/90273197-638d-43ac-8126-31bd37dd6af0/e4e04759-64a3-404a-b14c-15648798149c/zl9j05_thumbnail.png)
Transcribed Image Text:### Transcription of Educational Content
#### Problem Statement:
- There are two triangles that can be formed from the given information.
#### Triangle 1:
- **Angle A**: \( \approx \) [input box] \( ^\circ \)
- **Angle B**: \( \approx \) [input box] \( ^\circ \)
- **Side b**: \( \approx \) [input box]
#### Triangle 2:
- **Angle A**: \( \approx \) [input box] \( ^\circ \)
- **Angle B**: \( \approx \) [input box] \( ^\circ \)
- **Side b**: \( \approx \) [input box]
#### Explanation:
The task is to determine the angles and side length for two possible triangles based on some given information. The angles and sides are denoted by input boxes where values need to be provided. Each triangle's angles (A and B) and one side (b) need to be estimated.
The diagrams are absent, but the layout suggests boxes to fill in the answers for the angles (in degrees) and the side length.
### Analytical Steps:
1. **Enter the approximate values for angles A and B, ensuring they sum up to less than \(180^\circ\).**
2. **Input the lengths of side b for both triangles.**
3. **Verify that the triangles formed are valid and adhere to the triangle inequality theorem.**
This layout is useful in understanding the ambiguity in forming triangles given partial data and teaches the application of angle and side relations in geometry.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Recommended textbooks for you
 Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON
Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning