write a c++ code please test it Quadratic equations are the polynomialequations of degree 2 in one variable of typef(x) = ax²+bx+c. Where a, b, c, ER anda * 0. It is the general form of a quadraticequation where 'a' is called the leadingcoefficient and 'c' is called the absolute term off(x).The roots of a quadratic equation are thevalues of the variable that satisfy the equation.They are also known as the "solutions" or"zeros" of the quadratic equation. For example,the roots of the quadratic equationx²7x + 10 are *₁ = 2 and ₂- 5because they satisfy the equation (i.e. wheneach of them is substituted in the givenequation we get 0).The first step to solve the equation is to findthe determinant which equals 6² 4ac. Basedon the determinant value, we have threepossibilities for the equation roots:●If determinant > 0, the equation has tworeal and different roots which are:x1 =and-b-√determinant2a-b+√determinantx2 =2aIf determinant = 0, the equation has one-breal root which is: x =2a• If determinant < 0, then the equation hastwo complex (i.e. not real) roots which✓determinant-i and2aare: x1 =-b2aX2=-b2adeterminant2a•∙i.In this question, you are asked to write aprogram that finds the roots of any quadraticequation. The program requests the user toinsert the three coefficients a, b, and c,respectively and outputs the values of theroots as follows:• If there are two real different roots, theprogram prints the root ₁ then the root2 with a single space between them.• If there is a single real root, the programprints the root only once.• If there are two complex different roots,the program prints the root ₁ then theroot x2 on a new line.) ise1/0S1/0• 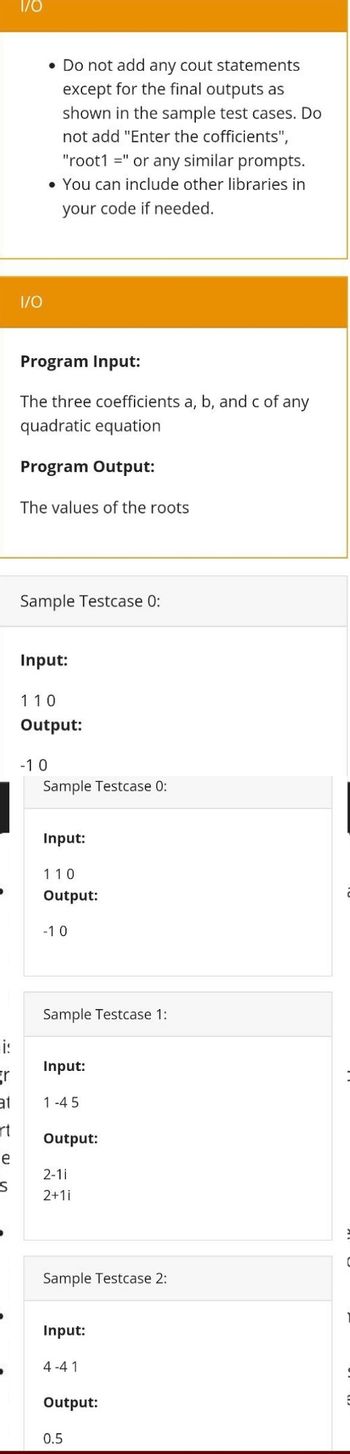Do not add any cout statementsexcept for the final outputs asshown in the sample test cases. Donot add "Enter the cofficients","root1 =" or any similar prompts.• You can include other libraries inyour code if needed.Program Input:The three coefficients a, b, and c of anyquadratic equationProgram Output:The values of the rootsSample Testcase 0:Input:110Output:-10Sample Testcase 0:Input:110Output:-10Input:grat 1-45rtSample Testcase 1:Output:2-112+1iSample Testcase 2:Input:4-41Output:0.5CE

We need to provide C++ code to find roots of quadratic equations.

In this question, you are asked to write a program that finds the roots of any quadratic equation. The program requests the user to insert the three coefficients a, b, and c, respectively and outputs the values of the roots as follows: • If there are two real different roots, the program prints the root x1 then the root X2 2 with a single space between them. • If there is a single real root, the program prints the root only once. If there are two complex different roots, the program prints the root ₁ then the root x2 on a new line.

In this question, you are asked to write a program that finds the roots of any quadratic equation. The program requests the user to insert the three coefficients a, b, and c, respectively and outputs the values of the roots as follows: • If there are two real different roots, the program prints the root x1 then the root X2 2 with a single space between them. • If there is a single real root, the program prints the root only once. If there are two complex different roots, the program prints the root ₁ then the root x2 on a new line.

Database System Concepts

7th Edition

ISBN:9780078022159

Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Publisher:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Chapter1: Introduction

Section: Chapter Questions

Problem 1PE

See similar textbooks

Similar questions

In C++ fill in the blanks
In C++ coding please 13.4 Programming 4: Binary Conversion In this assignment you will read in a string of 0's and 1's, you will then convert this to its decimal integer value and print that value on a single line (ending with a newline). For example: INPUT:0010 OUTPUT:2
In C++ write a program to perform all mathematical operations on two variables?
Hw// Write a program in C++ to calculate the value of the result of the series
Q3: Write a C++ code of an integer function that has two integer parameters passed by reference, and returns the remainder (mode) of the first parameter divided by the second parameter. *
answer in c++
make a program in c++ using the for. tool The user enters a number of numbers The program calculates the average for these numbers
Complete the toupper() function in C++ which takes a character as parameter and return the ASCII value of uppercase alphabet of the input parameter.int toupper(char );
C++ CODE
name is : reem
string is a primitive type of C++ True False
Exercise 2: Please perform in C++ Write a function that receives two numbers as an argument and display all prime numbers between these two numbers. Call this function from the main function. ●