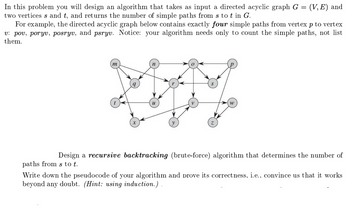
In this problem you will design an algorithm that takes as input a directed acyclic graph G two vertices s and t, and returns the number of simple paths from s tot in G. = (V,E) and For example, the directed acyclic graph below contains exactly four simple paths from vertex p to vertex v: pov, poryv, posryv, and psryv. Notice: your algorithm needs only to count the simple paths, not list them. m W

The given inputs consist of two nodes (s, t) and a directed graph G = (V, E). In addition, each edge of the graph is either blue or red. The goal is to find a path from point s to point t such that red edges always follow blue edges. There need not be any red or blue borders on the route, but if there are, the red ones should follow the blue ones. Develop an algorithm that does the task in O(n + m) time and analyze its performance.

If there is an Euler path that starts at AA and ends at some other vertex, give it. Otherwise enter DNE.This should be a list of letters, from A to the other vertex: e.g. ACBDEAD (if that were even possible!). Path:  Since this is a planar graph, the number of regions - arcs + nodes equals what number?

(V, E) be a connected, undirected graph. Let A = V, B = V, and f(u) = neighbours of u. Select all that are true. Let G = a) f: AB is not a function Ob) f: A B is a function but we cannot always apply the Pigeonhole Principle with this A, B Odf: A B is a function but we cannot always apply the extended Pigeonhole Principle with this A, B d) none of the above

3. Kleinberg, Jon. Algorithm Design (p. 519, q. 28) Consider this version of the Independent Set Problem. You are given an undirected graph G and an integer k. We will call a set of nodes I "strongly independent" if, for any two nodes v, u € I, the edge (v, u) is not present in G, and neither is there a path of two edges from u to v. That is, there is no node w such that both (v, w) and (u, w) are present. The Strongly Independent Set problem is to decide whether G has a strongly independent set of size at least k.   Show that the Strongly Independent Set Problem is NP-Complete.

You are given a weighted, undirected graph G = (V, E) which is guaranteed to be connected. Design an algorithm which runs in O(V E + V 2 log V ) time and determines which of the edges appear in all minimum spanning trees of G. Do not write the code, give steps and methods. Explain the steps of algorithm, and the logic behind these steps in plain English

Alert dont submit AI generated answer.   Write a program that reads a weighted graph and an initial vertex.The program must print on the screen the minimum paths obtained by Dijkstra's algorithm. Input: Receives n, m and s; n is the total number of vertices, m the total number of arcs and s is the initial vertex.Next, m lines, each line with a trio of integers, corresponding to the beginning and end of the arc, followed by the weight of the arc.(Vertices are identified from 0 to n-1.) Output: Prints the shortest paths obtained by Dijkstra's algorithm. Exemple: Input: 5 10 00 1 100 4 51 2 11 4 22 3 43 2 63 0 74 1 34 2 94 3 2 Output: [0, 8, 9, 7, 5][-1, 4, 1, 4, 0]

Please help me with this!!

Suppose you have a graph with 100 nodes and 500 edges and you want to find the shortest path between two nodes using Dijkstra's algorithm. What is the time complexity of this operation?

You are organizing a programming competition, where contestants implement Dijkstra's algorithm. Given adirected graph G = (V, E) with integer-weight edges and a starting vertex s ∈ V , their programs are supposedto output triplets (v, v.d, v.π) for each vertex v ∈ V . Design an O(V +E) time algorithm that takes as inputthe original graph G in both adjacency matrix (G.M) and adjacency list (G.Adj) representations, startingvertex s, and the output of a contestant's program (given as an array A of triplets), and returns whetherA is the correct output for G. Write down the pseudocode for your algorithm, explain why it correctlyveries the output, and analyze your algorithm's running time. You may assume that all edge weights of the input graph provided to the contestantsare nonnegative and A (the output of their programs) is in the valid format, i.e., you don't need to verifythat A is actually an array of triplets, with v and v.π being valid vertices and v.d being an integer.Can you…