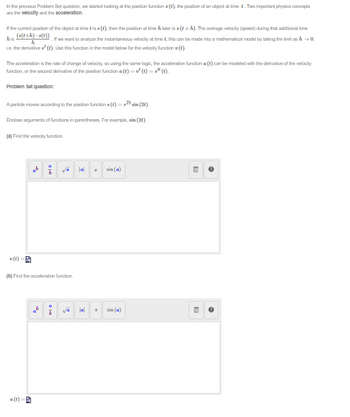
In the previous Problem Set question, we started looking at the position function (), the position of an object at fimet. Two important physics concepts are the velocity and the acceleration. If the current position of the object at time t is s (t), then the position at time later is s(t+h). The average velocity (speed) during that additional time his ("(t+h)-a(t)) If we want to analyze the instantaneous velocity at time t, this can be made into a mathematical model by taking the limit as h→0. L.e. the derivative a' (t). Use this function in the model below for the velocity function (t). The acceleration is the rate of change of velocity, so using the same logic, the acceleration function a (1) can be modeled with the derivative of the velocity function, or the second derivative of the position function a(t)=√(t)=s" (t). Problem set question: =e7t sin (21). A particle moves according to the position function (t) = Enclose arguments of functions in parentheses. For example, sin (21).

The position of a honeybee flying up and down a straight flowerbed is given by (the euqation ) where t is measured in seconds and s is measured in meters. Positive values of s indicate that the bee is to the right of the center of the flowerbed, while negative values of s indicate that it is to the left of the center. (a) Use the graph to guess the time(s) at which the velocity of the bee is 0, and then use calculus to confirm the answer (b) How fast and in what direction is the bee flying at t = 3.5 seconds?  (c) Find the velocity of the bee at all times when its acceleration is zero.

An automobile, traveling at a constant rate, starts at home at time t = 0 and ends up 10 hours later 200 miles from home. It than changes speed and continues for the next 10 hours ending up 300 miles from home. It takes another 10 hours for it to return home. On two separate set of axes, sketch graphs of the distance and velocity functions.

Section 4.1 Question 19 Part 1 of 5 I need help and the answers, thanks!