In the plane, there's a vector v=<a,b>. Find a unit vector that would maximize and a vector that would minimize v • u. What unit vectors would make v • u = 0? That's all there is. Thanks.
In the plane, there's a vector v=<a,b>.
Find a unit vector that would maximize and a vector that would minimize v • u. What unit
That's all there is. Thanks.
We are given that v=<a,b>. So, we can treat a and b can be treated as constant.
Let us take a vector u = <x, y>.
So, v • u = ||v|| ||u|| cos(θ) where θ is the angle between the vectors u and v.
Now, we need to find the values of x and y such that u will be a unit vector and v • u will be maximum. Similarly, for the minimum of v • u.
Note:
<x, y> is rotated by an angle θ then the resultant vector will be
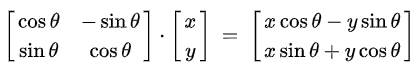 .
.
For maximum:
Note that v • u = ||v|| ||u|| cos(θ) will be maximum only when θ = 0.
We are given that ||u|| is a unit vector.
So,
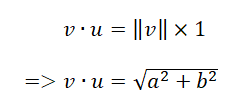
The value of v • u will be maximum whenever a2+b2 will be maximum. But a and b are fixed points.
Thus, any unit vector v which makes an angle 0 with the taken vector <a, b>, will make v • u maximum.
The simplest example can be taken as,
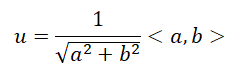 .
.
Step by step
Solved in 4 steps with 6 images









