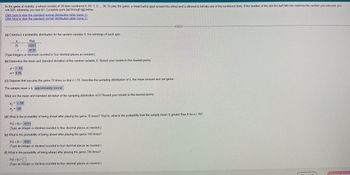
In the game of roulette, a wheel consists of 38 slots numbered 0, 00, 1. 2. 36. To play the game, a metal ball is spun around the wheel and is allowed to fall into one of the numbered slots. If the number of the slot the ball falls into matches the number you selected, you win $35, otherwise you lose $1. Complete parts (a) through (g) below Click here to view the standard normal distribution table (page 1) Click here to view the standard normal distribution table (page 2) (a) Construct a probability distribution for the random variable X, the winnings of each spin P(x) 0263 X 35 -1 9737 (Type integers or decimals rounded to four decimal places as needed.) (b) Determine the mean and standard deviation of the random variable X. Round your results to the nearest penny, H=-05 0 5.76 (c) Suppose that you play the game 70 times so that n=70. Describe the sampling distribution of x, the mean amount won per game. The sample mean x is approximately normal. What are the mean and standard deviation of the sampling distribution of x? Round your results to the nearest penny H=-05 0.69 (d) What is the probability of being ahead after playing the game 70 times? That is, what is the probability that the sample mean is greater than 0 for n=70? P(x>0) = 4711 (Type an integer or decimal rounded to four decimal places as needed.) (e) What is the probability of being ahead after playing the game 140 times? P(x>0)= 4591 (Type an integer or decimal rounded to four decimal places as needed.) (f) What is the probability of being ahead after playing the game 700 times? P(X>0)= (Type an integer or decimal rounded to four decimal places as needed.) Clear all Check answe

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.