
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Use the examples in the slides to answer the question.

Transcribed Image Text:In the game of poker played with an ordinary deck of 52 cards various five-card holdings are given special names. The name "three of a kind" is reserved for a holding
that meets the following rule:
Three cards of the same denomination and two other cards of different denominations.
The number of distinct "three of a kind" that can be drawn from a 52-card deck can be calculated with the following product expression:
(²
12) (4)
2
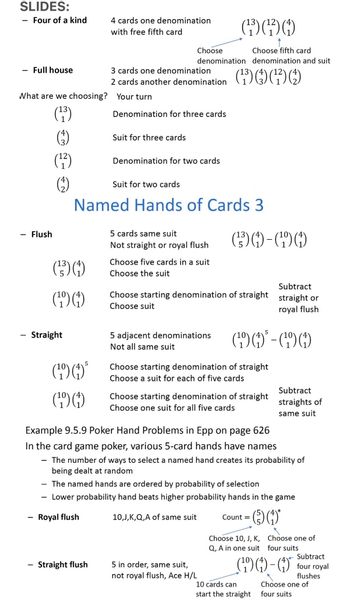
Transcribed Image Text:SLIDES:
-
Four of a kind
Full house
Flush
What are we choosing? Your turn
(¹3)
(¹2)
(33)()
(¹9) (4)
Straight
5
4 cards one denomination
with free fifth card
(19)9)
(¹9) (4)
3 cards one denomination
2 cards another denomination (¹3)(3)(¹)()
Denomination for three cards
Suit for three cards
Straight flush
Choose
Choose fifth card
denomination denomination and suit
Suit for two cards
Named Hands of Cards 3
Denomination for two cards
5 cards same suit
Not straight or royal flush
(30)
Choose five cards in a suit
Choose the suit
5 adjacent denominations
Not all same suit
13
Subtract
Choose starting denomination of straight straight or
Choose suit
royal flush
(34)-(0)
5
(¹9) (4) ³ - (94)
Choose starting denomination of straight
Choose a suit for each of five cards
5 in order, same suit,
not royal flush, Ace H/L
Choose starting denomination of straight
Choose one suit for all five cards
Example 9.5.9 Poker Hand Problems in Epp on page 626
In the card game poker, various 5-card hands have names
The number of ways to select a named hand creates its probability of
being dealt at random
The named hands are ordered by probability of selection
Lower probability hand beats higher probability hands in the game
Royal flush
10,J,K,Q,A of same suit
(*
Count =
Subtract
straights of
same suit
Choose 10, J, K,
Q, A in one suit
10 cards can
start the straight
Choose one of
four suits
(49)0)-(
Subtract
four royal
flushes
Choose one of
four suits
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Please show me how to answer in excel. Questions 3-6.arrow_forwardMatch these values of r with the accompanying scatterplots: - 0.385, 0.385, 0.997, - 0.767, and 1. Click the icon to view the scatterplots. Match the values of r to the scatterplots. Scatterplots Scatterplot 1, r = 0.385 Scatterplot 2, r= 0.997 Scatterplot 3, r = -0.767 Scatterplot 4, r = Scatterplot 1 Scatterplot 2 Scatterpl 8- R- 8- - 0.385 6- 6- 6- Scatterplot 5, r= 1 > 4- 4- 4- 2- 2- b- 0- 0- 0.2 0.4 0.6 0.8 1 0.2 0.4 0.6 0.8 1 0.2 0.4 0.6 х х Scatterplot 4 Scatterplot 5 15- 8- 14- 6- 13- 4- 12- 2- 11- 10- 0+ 1 0.2 0.4 0.6 0.8 0.2 0.4 0.6 0.8 хarrow_forwardDr. Dorothy Smith gave the students in her geometry class at the University of New Orleans the following question. Is it possible to construct a triangle such that the second angle of the triangle has a measure that is twice the measure of the first angle and the measure of the third angle is 5 times the measure of the first? If so, find the measure of each angle.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education