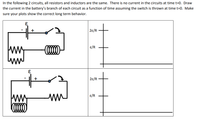
**Educational Content on RL Circuits**In the following two circuits, all resistors and inductors are the same. Initially, there is no current in the circuits at time \( t=0 \). Your task is to draw the current in the battery's branch of each circuit as a function of time, assuming the switch is thrown at time \( t=0 \). Ensure your plots depict the correct long-term behavior.### Circuit Diagrams:#### First Circuit (Top):- The circuit consists of a battery (\( \epsilon \)), a resistor, an inductor, and a switch.- Upon closing the switch at \( t=0 \), the current begins to flow, affected by the resistance and inductance.#### Second Circuit (Bottom):- Similar to the top circuit, this one also includes a battery (\( \epsilon \)), a resistor, an inductor, and a switch.- When the switch is closed at \( t=0 \), the behavior mirrors the first circuit initially, with the current developing over time due to the resistance and inductance present.### Graphs to Illustrate Current Over Time:For both circuits, the right-hand side contains graphs representing current as a function of time:- **Vertical Axis (Current):** - Points marked at \( \frac{2\epsilon}{R} \) and \( \frac{\epsilon}{R} \).- **Horizontal Axis (Time):** - Time progresses to the right, showing how current stabilizes over time.Both circuits display curves that start from zero current and adjust according to the characteristics of the resistor and inductor, illustrating how the current stabilizes to its final value over time. The graphs should show an exponential rise in current as \( t \) increases, ultimately reaching the steady-state where the inductor behaves like a short circuit. For educational purposes, note how the inductance initially resists changes in current, causing the exponential growth and eventual settling of the current at long-term values.

Answered: Image /qna-images/answer/fd7b6c83-6283-4cdd-b282-1d796431f146.jpg

In the following 2 circuits, all resistors and inductors are the same. There is no current in the circuits at time t=0. Draw the current in the battery's branch of each circuit as a function of time assuming the switch is thrown at time t=0. Make sure your plots show the correct long term behavior. + 26/R ɛ/R + 2ɛ/R E/R

In the following 2 circuits, all resistors and inductors are the same. There is no current in the circuits at time t=0. Draw the current in the battery's branch of each circuit as a function of time assuming the switch is thrown at time t=0. Make sure your plots show the correct long term behavior. + 26/R ɛ/R + 2ɛ/R E/R

Introductory Circuit Analysis (13th Edition)

13th Edition

ISBN:9780133923605

Author:Robert L. Boylestad

Publisher:Robert L. Boylestad

Chapter1: Introduction

Section: Chapter Questions

Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...

See similar textbooks

Similar questions

The Insulator has a very small energy gap ? True O False O
Calculate the inductance for a coil with 120 turns, a current of 0.47 mA, and a flux of 1.2x10 Wb. b H a S ww R
What is the resistance to the changing flow of alternating current? Select one: A. AMPERES B. INDUCTANCE C. REACTANCE
In a semiconductor crystal, the atoms are held together by Forces of attraction The interaction of valence electrons Covalent bonds lonic bonds
Answer part (D)
When the voltage source is turned off in a simple circuit consists of a resistor and an inductor, the rate of decrease of the current is proportional to the current. The current is 40 amperes at the moment that the switch is off and dies down to 15 amperes after 0.01 sec. Determine the current in 0.02 sec. 3.375 amperes 4.25 amperes 5.625 amperes 6.025 amperes
How much energy must a 24-V battery expend to chargea 0.45 µ F and a 0.20µ F capacitor fully when they areplaced (a) in parallel, (b) in series? (c) How much chargeflowed from the battery in each case?
Write down the steps on how to Series Resistors Voltage Division
An ammeter has been designed by indirect method with current ranges 1A, and 5A, if PMMC meter have internal resistance of 50 (2 and half scale current of 0.5 mA. Ra and Rb will be --- ohm Ra= 0.05005 , Rb=0.01001 Ra = 0.04004 , Rb = 0.01001 Ra= 0.05005 Rb= 0.04004
When the switch is closed in above circuit, what is the voltage on the inductor, resistor R1 and R2 after 2.2us , assuming 0 V on the inductor to start?
Calculate the equivalent resistances Rin of the following circuits. (The resistance value of the diodes in the conduction will be 0, the resistance value of the diodes in the insulation will be taken as infinity. R1=10ohm
According to the circuit what is the best answer for bullet 2-4?