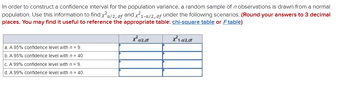
In order to construct a confidence interval for the population variance, a random sample of n observations is drawn from a normalpopulation. Use this information to find x²a/2, df and x²1-a/2, df under the following scenarios. (Round your answers to 3 decimalplaces. You may find it useful to reference the appropriate table: chi-square table or Ftable)X²al2,dfa. A 95% confidence level with n = 9.b. A 95% confidence level with n = 40.c. A 99% confidence level with n = 9.d. A 99% confidence level with n = 40.X²1-a/2,df

Hello! As you have posted more than 3 sub-parts, we are answering the first 3 sub-parts. In case…

Answered: In order to construct a confidence…

A First Course in Probability (10th Edition)

10th Edition

ISBN:9780134753119

Author:Sheldon Ross

Publisher:Sheldon Ross

Chapter1: Combinatorial Analysis

Section: Chapter Questions

Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...

See similar textbooks

Similar questions

An analysis of variance produces SSbetween = 40, SSwithin = 60, and an F-ratio with df = 2, 15. For this analysis, what is the F-ratio?
Listed below are altitudes (thousands of feet) and outside air temperatures (°F) recorded during a flight. Find the (a) explained variation, (b) unexplained variation, and (c) indicated prediction interval. There is sufficient evidence to support a claim of a linear correlation, so it is reasonable to use the regression equation when making predictions. For the prediction interval, use a 95% confidence level with the altitude of 6327 ft (or 6.327 thousand feet). Altitude 8 15 22 28 31 33 Temperature 56 39 24 - 28 - 41 - 60 a. Find the explained variation. (Round to two decimal places as needed.)
An ecologist is studying the impact of local polluted waters on the growth of alligators. The length of adult male alligators typically follows a normal distribution with a standard deviation of 2 feet. The ecologist wants to estimate the mean length of this population of alligators. Suppose she samples n alligators at random and uses the sample mean, X to as an estimator for u. a. What is the bias and variance of the estimator? (Note, these may be a function of n.) b. If n = 4, what is the probability that the estimator is within one foot of the true mean? (I.e. find P(|X – µ| < 1). c. What sample size, n, is required for the estimator to be within one foot of the true mean with 95% probability? (I.e. find the value of n that satisfies P(|X – µ| < 1) = 0.95.) d. Suppose the ecologist ends up sampling n = 9 alligators and calculates a sample mean of ī = 10.4 feet. Construct a 95% confidence interval for the population mean. e. Give an interpretation for the interval obtained in (d).
Our environment is very sensitive to the amount of ozone in the upper atmosphere. The level of ozone normally found is 6.3 parts/million (ppm). A researcher believes that the current ozone level is at an excess level. The mean of 870 samples is 6.4 ppm. Assume the variance is known to be 1.00. Does the data support the claim at the 0.1 level? Step 2 of 5 : Enter the value of the z test statistic. Round your answer to two decimal places.
A2
A physical therapist wanted to know whether the mean step pulse of men was less than the mean step pulse of women. She randomly selected 54 men and 70 women to participate in the study. Each subject was required to step up and down a 6-inch platform. The pulse of each subject was then recorded. The following results were obtained. Two sample T for Men vs Women N Mean StDev SE Mean Men Women 98% CI for mu Men - mu Women (- 12.20, - 1.00) T-Test mu Men = mu Women (vs H2 O C. Ho: H1 = H2; Ha: H1 #H2 (b) Identify the P-value and state the researcher's conclusion if the level of significance was a = 0.01. What is the P-value? P-value =
Two accounting professors decided to test if the variance of their grades is different or no. To accomplish this, they each graded the same 10 exams with the following results: Standard Grade þeviation 22.4 12.0 Мean Professor 1 Professor 2 79.3 82.1 F What is the P-value of the test? Select one: Oa. between 0.01 and 0.025 Ob. between 0.025 and 0.05 c. between 0.05 and 0.10 Od. bigger than 0.10
In the year 2032, Katie Ruff is a leading traveling nurse. Katie is interested in reducing the mean recovery time for patients after experiencing a serious injury. Suppose the mean recovery time is presently 8.4 months. Katie takes a random sample of 45 patients that have experienced serious injury to participate in a new treatment program and finds the sample mean is 7.9 months and a sample standard deviation of 1.2 months. Using α = 0.05, answer the following questions. a) What is the setup for your null and alternative hypothesis? b) What is the value of the test statistic? c) Using the appropriate level of confidence, what is the confidence interval? d) What is the interpretation (not your conclusions) in the context of the problem of the confidence interval you obtained in part c? e) What is the p value? f) What is the interpretation (not your conclusions) of the p value in the context of the problem you found in part…
Listed below are altitudes (thousands of feet) and outside air temperatures (°F) recorded during a flight. Find the (a) explained variation, (b) unexplained variation, and (c) indicated prediction interval. There is sufficient evidence to support a claim of a linear correlation, so it is reasonable to use the regression equation when making predictions. For the prediction interval, use a 95% confidence level with the altitude of 6327 ft (or 6.327 thousand feet). Altitude Temperature a. Find the explained variation. (Round to two decimal places as needed.) 2 55 8 40 13 25 20 - 3 28 - 26 31 - 41 34 - 53
You are testing the claim that having lights on at night increases weight gain (abstract). A sample of 10 mice lived in an environment with bright light on all of the time and 8 mice who lived in an environment with a normal light/dark cycle is given below. Test the claim using a 10% level of significance. Assume the population variances are unequal and that the weight changes are normally distributed. Give answers to 3 decimal places. Data available at StatKey, choose Mice Wgt Gain-2e data set Light (x₁) 1.71 4.67 4.99 5.33 5.43 6.94 7.15 9.17 10.26 11.67 What are the correct hypotheses? Note this may view better in full screen mode. Select the correct symbols in the order they appear in the problem. Ho: Select an answer ? V Select an answer V Ha: Select an answer ✓ Based on the hypotheses, find the following: Test Statistic = Dark (₂) 2.27 2.53 2.83 4 4.21 4.6 5.95 6.52 p-value = ? V Select an answer V (Hint: difference in means from Ha) The correct decision is to Select an answer…
Please answer the question contained in the following picture
One of the following is the minimum variance unbiased estimator for u. The sample variance. The sample mean. The sample mean square error. The meadian.

SEE MORE QUESTIONS

Recommended textbooks for you

A First Course in Probability (10th Edition)

Probability

ISBN:

9780134753119

Author:

Sheldon Ross

Publisher:

PEARSON

A First Course in Probability

Probability

ISBN:

9780321794772

Author:

Sheldon Ross

Publisher:

PEARSON

A First Course in Probability (10th Edition)

Probability

ISBN:

9780134753119

Author:

Sheldon Ross

Publisher:

PEARSON

A First Course in Probability

Probability

ISBN:

9780321794772

Author:

Sheldon Ross

Publisher:

PEARSON

SEE MORE TEXTBOOKS