In a certain school district, it was observed that 29% of the students in the element schools were classified as only children (no siblings). However, in the special program for talented and gifted children, 119 out of 346 students are only children. The school district administrators want to know if the proportion of only children in the special program is significantly different from the proportion for the school district. Test at the a = 0.05 level of significance. What is the hypothesized population proportion for this test? (Report answer as a decimal accurate to 2 decimal places. Do not report using the percent symbol.) Based on the statement of this problem, how many tails would this hypothesis test have? one-tailed test two-tailed test Choose the correct pair of hypotheses for this situation: (A) (B) (C) |Но:р 3 0.29 Ha:p < 0.29 Ho:p = 0.29 Ha:p + 0.29 Ho:p = 0.29 Ha:p > 0.29 (D) (E) (F) Но: р 3D 0.344 |Но:р 3 0.344 Но:р— 0.344 Ha:p < 0.344 Ha:p + 0.344 Ha:p > 0.344 0.344 Ho:p : (A) (B) (C) (D) (E) (F) Using the normal approximation for the binomial distribution (without the continuity correction), what is the test statistic for this sample based on the sample proportion? (Report answer as a decimal accurate to 3 decimal places.) You are now ready to calculate the P-value for this sample. P-value = (Report answer as a decimal accurate to 4 decimal places.) This P-value (and test statistic) leads to a decision to... Oreject the null accept the null Ofail to reject the null O reject the alternative As such, the final conclusion is that... There is sufficient evidence to warrant rejection of the assertion that there is a different proportion of only children in the G&T program. There is not sufficient evidence to warrant rejection of the assertion that there is a different proportion of only children in the G&T program. The sample data support the assertion that there is a different proportion of only children in the G&T program. There is not sufficient sample evidence to support the assertion that there is a different proportion of only children in the G&T program. Question Help: M Message instructor

Determine the hypothesized population proportion for the given test.

The hypothesized population proportion for the given test is determined below:

From the information, given that 29% of the student in the element schools were classified as only children.

Thus, the hypothesized population proportion for the given test is 0.29.

Determine the tail of the test for the given hypothesis test.

From the information, given the claim is proportion of the children in the special program is significantly different from the proportion for the district.

Thus, it is clear that direction of the tail for the given hypothesis test is two tailed

State the hypotheses.

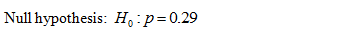
That is, there is no evidence that the proportion of the children in the special program is significantly different from the proportion for the district

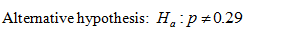
That is, there is evidence that the proportion of the children in the special program is significantly different from the proportion for the district

Decision rule:

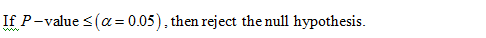
Correct option: Option B.

Obtain the value of the test statistic.

The value of the test statistic is obtained below:

From the information, given that

The required value is,

Thus, the value of the test statistic is 2.049