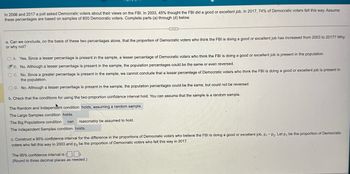
In 2008 and 2017 a poll asked Democratic voters about their views on the FBI. In 2003, 45% thought the FBI did a good or excellent job. In 2017, 74% of Democratic voters felt this way. Assume these percentages are based on samples of 800 Democratic voters. Complete parts (a) through (d) below. a. Can we conclude, on the basis of these two percentages alone, that the proportion of Democratic voters who think the FBI is doing a good or excellent job has increased from 2003 to 2017? Why or why not? OA. Yes. Since a lesser percentage is present in the sample, a lesser percentage of Democratic voters who think the FBI is doing a good or excellent job is present in the population. B. No. Although a lesser percentage is present in the sample, the population percentages could be the same or even reversed. OC. No. Since a greater percentage is present in the sample, we cannot conclude that a lesser percentage of Democratic voters who think the FBI is doing a good or excellent job is present in the population. OD. No. Although a lesser percentage is present in the sample, the population percentages could be the same, but could not be reversed. b. Check that the conditions for using the two-proportion confidence interval hold. You can assume that the sample is a random sample. The Random and Independent condition holds, assuming a random sample. The Large Samples condition holds. The Big Populations condition can reasonably be assumed to hold. The Independent Samples condition holds. c. Construct a 95% confidence interval for the difference in the proportions of Democratic voters who believe the FBI is doing a good or excellent job, p₁ - P2. Let p, be the proportion of Democratic voters who felt this way in 2003 and p2 be the proportion of Democratic voters who felt this way in 2017. The 95% confidence interval is (.). (Round to three decimal places as needed.)

Construct a confidence interval of the population proportion at the given level of confidence.   x=120​, n=1200​, 96​% confidence   What is the lower bound of confidence? What is the higher bound of confidence?

Construct a 96% confidence interval if x=75 and n=200. Round your answers to 3 decimal places.

Construct an  80 %  confidence interval for the mean height of sons whose fathers are  70  inches tall. Round your answer to at least three decimal places. An  80 %  confidence interval for the mean height of sons whose fathers are  70  inches tall is   (this is part 2 of 2 of the math problem, please and thank you

Construct a confidence interval for p1−p2 at the given level of confidence.   x1=368​, n1=523​, x2=441​, n2=593​, 95​% confidence The researchers are nothing​% confident the difference between the two population​ proportions, p1−p2​, is between nothing and nothing.

Help!

Length of a confidence interval. Which confidence interval would be shorter, a confidence interval computed using a sample size of 90 or a confidence interval computed using a sample size of 900? Assume that the confidence level is 95% for both confidence intervals and that the only difference between them is the sample size. Explain your reasoning.

7b) see picture

Question:     Part B. Construct a 95​% confidence interval of the mean pulse rate for adult males. __bpm <u<__bpm Multiple Choice: Compare the results. A. The confidence intervals do not​ overlap, so it appears that adult females have a significantly higher mean pulse rate than adult males. B. The confidence intervals​ overlap, so it appears that adult males have a significantly higher mean pulse rate than adult females. C. The confidence intervals do not​ overlap, so it appears that there is no significant difference in mean pulse rates between adult females and adult males. D. The confidence intervals​ overlap, so it appears that there is no significant difference in mean pulse rates between adult females and adult males.