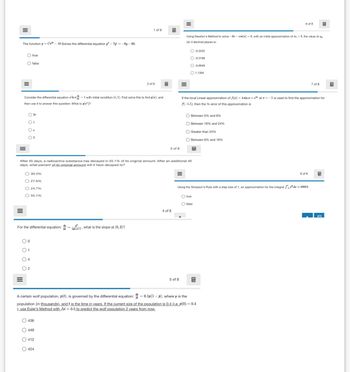
III The function y = Ce-10 Solves the differential equation 3"-7=-6y - 60. true false 6 of 8 1 of 8 Using Newton's Method to solve -3x-cos(x) = 0, with an initial approximation of z₁ = (to 4 decimal places is: the value of 2 of 8 Consider the differential equation In = 1 with initial condition (e, 1). First solve this to find y(2), and then use it to answer this question: What is y(e)? 2e ○ 1 ○ e 2 -0.3332 O-0.3168 -0.6948 1.1394 7 of 8 If the local Linear approximation of f(x)=4sin x+e at = -1 is used to find the approximation for f(-1.1), then the % error of this approximation is Between 0% and 8% Between 16% and 24% O Greater than 24% Between 8% and 16% 3 of 8 After 45 days, a radioactive substance has decayed in 55.1% of its original amount. After an additional 45 days, what percent of its original amount will it have decayed to? 30.4% 27.6% 24.7% 55.1% For the differential equation: +1, what is the slope at (0,2)? 01 ○ 4 ○ 2 8 of 8 Using the Simpson's Rule with a step size of 1, an approximation for the integral de 30852, true Ofalse 4 of 8 = A certain wolf population, p(t), is governed by the differential equation: 5 of 8 0.1p(1 - p), where p is the population (in thousands), and t is the time in years. If the current size of the population is 0.4 (i.e. p(0) = 0.4 ), use Euler's Method with At=0.5 to predict the wolf population 2 years from now. 436 449 412 424

Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...