Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
Please show all steps example is included
![Example 4 We use Taylor's formula to prove that, if f" -f=0 on R and
f(0) = f'(0) = 0, then f = 0 on R.
Since f" = f, we see by repeated differentiation that f(k) exists for all k; in
particular,
f(²)=ff
\ƒ'
is even,
if k
if k is odd.
Since f(0) = f'(0) = 0, it follows that f()(0) = 0 for all k. Consequently Theorem
4.1 gives, for each k, a point k = (0, x) such that
f(x) = R(x) =
Since there are really only two different derivatives involved, and each is con-
tinuous because it is differentiable, there exists a constant M such that
f(k+1)(x+1
(k + 1)!
|f(k+¹)(t)| ≤ M for te [0, x] and all k.
Hence f(x)| ≤ M\x|k+¹/(k + 1)! for all k. But limx→∞ x+¹/(k + 1)! = 0, so
we conclude that f(x) = 0.](https://content.bartleby.com/qna-images/question/a8d46346-fe9f-45aa-a3a0-df12b7cae379/d8f3589a-de5f-4927-b59c-fec7e565018b/3hm5w9f_processed.jpeg)
Transcribed Image Text:Example 4 We use Taylor's formula to prove that, if f" -f=0 on R and
f(0) = f'(0) = 0, then f = 0 on R.
Since f" = f, we see by repeated differentiation that f(k) exists for all k; in
particular,
f(²)=ff
\ƒ'
is even,
if k
if k is odd.
Since f(0) = f'(0) = 0, it follows that f()(0) = 0 for all k. Consequently Theorem
4.1 gives, for each k, a point k = (0, x) such that
f(x) = R(x) =
Since there are really only two different derivatives involved, and each is con-
tinuous because it is differentiable, there exists a constant M such that
f(k+1)(x+1
(k + 1)!
|f(k+¹)(t)| ≤ M for te [0, x] and all k.
Hence f(x)| ≤ M\x|k+¹/(k + 1)! for all k. But limx→∞ x+¹/(k + 1)! = 0, so
we conclude that f(x) = 0.
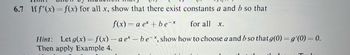
Transcribed Image Text:6.7 Iff"(x)=f(x) for all x, show that there exist constants a and b so that
f(x)= a ex+be-*
for all Xx.
Hint: Let g(x)=f(x) - ae* - be-*, show how to choose a and b so that g(0) = g'(0) = 0.
Then apply Example 4.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps
Knowledge Booster
Similar questions
- 5- -5 5 -5- Determine the values of a, b, c, and d so the function (a - a) (x + 1) (x + b) (x- c) (x + d) (x + 3) f (x) = correctly model the graph. (a, b, c, and d are all whole numbers) a = 5,arrow_forwardWhat is the range of the 2,3,-5,4,14arrow_forwardExplain conditions for use of the t-procedures?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,