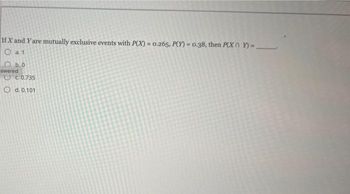
If X and Y are mutually exclusive events with P(X) = 0.265, P(Y) = 0.38, then PCX Y)= O a. 1 b.0 swered C. 0.735 O d. 0.101
Q: A contractor is required by a county planning department to submit one, two, three, four, five, six,…
A:
Q: Assume that 12 jurors are randomly selected from a population in which 76% of the people are…
A: The probability distribution table is given as: X P(x) 0 0+ 1 0+ 2 0+ 3…
Q: Suppose Q and R are independent events, and P(Q) = 0.39, P(R) = 0.85. Find P(Q and R). a Ob OC Od…
A: It is given that P(Q) = 0.39P(R) = 0.85The events Q and R are independent events.
Q: A contractor is required by a county planning department to submit one, two, three, four, five, six,…
A:
Q: What is the correlation p between X and Y for the joint probability table?
A:
Q: x P(x) 0 0.186 1 0.417 2 0.242 3 0.131 4 0.021 5 0.003 a. Find the probability of getting exactly 4…
A: We have to choose ckrrect options.
Q: ycle at a proposed left turn lane is displayed in the accompanying joint probability table. Y XY 1…
A:
Q: 0 |2 4 | 6 P(X = x) a a
A: Identify the correct option to obtain the correct value of the probability P. The correct option to…
Q: do №%₂ 6 should Cards r) find the 1) probability PPP) None адачу. are drawn from probability of…
A: Here, X~Bin (n,p) P(X=x)=Cxnpx(1-p)n-x where, x=0,1,2,3,.....,n. Cxn=n!x!×(n-x)! where,…
Q: Suppose that 20,000 married adults in a country were randomly surveyed as to the number of children…
A: We have given that 20,000 married adults in a country were randomly surveyed as to the number of…
Q: The table below lists the probabilities associated with 5 mutually exclusive events. Given an event…
A: Given: P(A)=0.2309P(B)=0.1422P(C)=0.2859P(D)=0.1188P(E)=0.2222
Q: Ex 1. There are two machines available for cutting corks intended for use in wine bottles. The first…
A: General guidance Concepts and reason Normal distribution: Normal distribution is a continuous…
Q: Let X be a regular random variable, then V( E(X)) = OA. V(X). O B. some positive number. OC. EX).…
A: Random variables are of 2 types, discrete and continuous. A discrete random variable can only take…
Q: Suppose that 20,000 married adults in a country were randomly surveyed as to the number of children…
A: Let X be the random variable having probability mass function then we will find the expected value…
Q: A contractor is required by a county planning department to submit one, two, three, four, five, six,…
A:
Q: Suppose X and Y have the joint probability distribution given by the table shown below. Compute…
A:
Q: 1. Let X be a random variable with the following probability distribution. 1 2 3 4 P(X=x) 0.4 0.3…
A: Given Information: X 1 2 3 4 P(X) 0.4 0.3 0.2 0.1 Mean or Expected value is obtained using…
Q: Assume A and B are independent events with P(A) = 0.1 and P(B) = 0.3. Find (a) P(A N B), (b) P(A U…
A:
Q: Consider three types of claims: A, B and C. Let XẠ denote the rand variable for the size of a…
A: a) From the given information, An insurance company has a portfolio of policies with 10% of claims…
Q: 11. Let X be a random variable with the following probability distribution: t X f(x) -3 6 2 9 T 3…
A: From the provided information,The probability distribution is as follow:x-369f (x)1/61/21/3
Q: ents C and D for which P(C)=0.75 and P(D)=0.8 and P(CUD')=0.15
A: Given that C and D are two events. P(C)=0.75 ; P(D)=0.8 ; P(CUD')=0.15 By addition theorem we know…
Q: J and K are independent events. P(J | K) = 0.17. Find P(J) P(J) =
A:
Q: Let event C=taking an English class. Let event D=taking a mathematics class. Suppo P(C) =0.75,…
A: The question is about probability of events Given : C : Taking an English class D : Taking a…
Q: Given that P(E) = 0.8, what must be true about the event E?
A: P(E) = 0.8
Q: Let X be the number of students who show up for a professor's office hour on a particular day.…
A: Probability of an event is computed by taking the ratio of number of favourable outcomes to total…
Q: The joint probability distribution of variables X and Y is shown in the table below, where X is the…
A: We know, EXY=∑i∑jxi×yj×fx,y =1×1×0.14+1×2×0.04+2×1×0.03+2×2×0.13 + 0 =0.8 From…
Q: 1. In one city, 23% of the population is under 25 years of age. Three people are selected at random…
A:
Q: Suppose that the random variable x, shown below, represents the number times. P(x) represents the…
A:
Q: 4. The probability function of a d.a.d. X is: img. The expected value of X is E(X)= ? The…
A: Given function is f(x)=2x+125 ; x=0,1,2,3,4
Q: The random variables X1,..., Xn are independent and identically distributed with probability…
A: Given information: The probability density function of the random variables X and Y is given.
Q: let Y be a random variable that can either be equal to 0 to 1. let p(Y=1)=p,what is E(|Y-p|)?
A:
Q: 11.The distribution function of a random variable is 1 fæ =(x – 1)* ,1< x < 3 then the probability…
A: Introduction :- Let X be a random variable. Weare given a cumulative distribution function for X.…
Q: y? (d) Could p(y) = for y = 1, .., 7 be the pmf of Y? 136 ---Select--- v P(Y) = because P(V) y = 1
A: Given that p(y)=(y2/136) for y=1,2,___,7
Q: U and V are mutually exclusive events. P(U)=0.15 ; P(V)=0.49 Find P(U orV) =
A: Two events U and V are said to be mutually exclusive events when both cannot occur at the same time.
Q: Suppose two independent discrete random variables X₁ and X2. Both follow a discrete distribution…
A: It is given that: PX1=1=PX2=1=p1=0.5PX1=2=PX2=2=p2=0.3PX1=3=PX2=3=p3=0.2 The variables X1 and X2 are…
Q: contractor is required by a county planning department to submit one, two, three, four, five, or six…
A: Probability mass function of Y is p(y)=ky , y=1,2,3,4,5,6Note: According to bartelby question answer…
Q: Ex. 2. A random variable X is exponentially distributed with the deviance 1/4. Compute the…
A:
Q: 3. The following table lists the probability function of the discrete variables (X, Y). Known that…
A:
Q: Suppose the random variable X has the following probability distribution -1 1 P(X=x) 0.2 0.3 0.3 0.2…
A: Given data, 1)P(X<2)=?
Q: A contractor is required by a county planning department to submit one, two, three, four, or five…
A: givenY: the number of forms required of the next applicant.given probability density fuction of…
Q: 1. 1. Express P(A) in terms of x. 2. Express P(B) in terms of x. 2. Find the value of x. 3. Find…
A:
Step by step
Solved in 3 steps with 1 images
- Here's a discrete probability experiment: a college instructor keeps track of the number of students who come in during her office hours. In the table, x is the number of students who visit her during her office hours, and P(x) is the associated probability. P(x) 0.25 0.15 0.25 0.35 (a) Find the probability that at least one student comes in during office hours. (b) Find the probability that NO students come. (c) What word do we use to denote the relationship of the events described in (a) and (b)? O skewed O complements O correlated O independent (d) What's the average number of students the instructor can expect to come in during office hours? Don't round your answer. students, on averageLet A and B be two independent events with P(A) = 0.25 and P(AU B) = 0.75. Then, the value of P(A – B) is O0.33333 00.08333 00.5 0.125Pr. 3 Production. In a production process, let N mean "no trouble" and T"trouble." Let the transition probabilities from one day to the next be 0.8 for N ->>> N, hence 0.2 for N ->>> T, and 0.5 for T → N, hence 0.5 for T→ T. If today there is no trouble, what is the probability of N two days after today? Three days after today?
- Let X be the number of random number of cars and the Y be the number of buses per signal cycle at a proposed left turn lane is displayed in the accompanying joint probability table. Y X/Y 1 2 0.025 0.015 0.010 1 0.050 0.030 0.020 2 0.125 0.075 0.050 3 0.150 0.090 0.060 4 0.100 0.060 0.040 5 0.050 0.030 0.020 Find the probability that there is exactly two cars and exactly one bus during a cycle? What is the probability that there is almost one car and at most one bus during a cycle? What is the probability that there is exactly one car during a cycle? Exactly one bus?A contractor is required by a county planning department to submit one, two, three, four, five, or six forms (depending on the nature of the project) in applying for a building permit. Let Y = the number of forms required of the next applicant. The probability that y forms are required is known to be proportional to y-that is, p(y) = ky for y = 1, ..., 6. (Enter your answers as fractions.) (a) What is the value of k? [Hint: S P(Y) = 1] y = 1 k = (b) What is the probability that at most three forms are required? (c) What is the probability that between two and five forms (inclusive) are required? (d) Could p(y) = for y = 1, ..., 6 be the pmf of Y? 92 ---Select--- v because p(y) = y = 1The random variable X can take on the values 2, 4 and 6, and the random variable Y can take onthe values 2, 6 and 10. Their joint probability distribution is given by the following table:Y2 6 10X2 0.10 0.05 0.104 0.10 0.15 0.256 0.10 0.10 0.05a. Describe in words and notation the event that has probability 0.25 in the table.b. Calculate the marginal distribution of X.c. Calculate ?ሺ? 4ሻ.d. Calculate the population mean of X.e. Calculate the conditional distribution of Y given X=2.f. Calculate E(Y|X=2).
- 3. Consider two evénts A and B such that Pr(A) = 1/3 and Pr(B)= 1/2. Determine the value of Pr(B 0A) for each of the following conditions: (a) A and B are disjoint: (b) AC B: (c) Pr(A O B)= 1/8.2. Let X be the mean of a random sample of n = 25 from N(30, 9). Find the probability that the sample mean is between 29.8 and 30.6.DO OD. None of the above 14. If X is distributed as Binomial with n = 9 and p = 0.45, then the probability that X is at least 0 and at most 9 is O O Ο Α. 0 O B. (0.45)^9 C. 1 OD. (0.45)(9) 15. Let A and C be independent events, with P(A) = 1/3 and P(C) = 4, then P(AUC) is O A. 7/12 O O O nined B. 1/2 C. 0 OD. 5/12 16. Let A and C be mutually exclusive events with P(A) = 3/8, P(C) = 1/8, AU C) = ½2, then P(AC) is
- Given X and Y are two events. LetP(M)= 0.49, P(N) = 0.44, P(MN) = 0.17 Find the value of P(M/N'),given M and N are two events.Let X₁ and X₂ be independent r.v.'s having the same distribution, taking on values 0 and 1 with respective probabilities 0.2 and 0.8. Answer Questions 12 and 13 below. Question 12 Write the m.g.f. of X₁ + X₂ + 2. (0.2+0.8e²) ²% e²z ○ (0.2e + 0.8e²x) e²z (1 + 0.² e² )² e²² (0.2+0.8e²)² e²z Question 13 Write the m.g.f. of X₁ – 2X₂. (0.2 +0.8e²) (0.2 +0.8e-2²) (0.8e + 0.2e²) (0.2e + 0.8e-2²) (0.2e +0.8e²) (0.2e-² +0.8e-²²) O (0.2e² +0.8e-²) (0.2e + 0.8e²)Solve the below problem. Table 1 contains the probabilities associated with each possible pair of values for Y, and Y, and is known as the joint probability function for Y,and Y2 Table: Probability function for Y, and Y, Yı_ y2 0 1 2 0 1/9 2/9 1/9 2/9 2/9 0 1 | 2 1/9 0 Find F (1, –2) and F(3,3).
