Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Course Name: Calculus with Analytical Geometry-1 Course Code: MATH 132 Do not use Artificial…
A: For a function to be continuous at a point, the left-hand limit, right-hand limit, and the value of…
Q: please full solution thank youu
A: More explain
Q: please full solution
A: Python-based solution: Python code: import sympy as sp# Define symbolsx, y, z = sp.symbols('x y…
Q: Proposition For any 5 € S, the set stab(s) is a subgroup of G. Proof (outline) To show stab(s) is a…
A:
Q: 8. Answer these two questions: a) If a tree has four vertices of degree 2, one vertex of degree 3,…
A: FEEL FREE TO ASK FOR CLARIFICATIONS
Q: Assist me with writing the permutation using attachment below
A: FEEL FREE TO ASK FOR CLARIFICATIONS
Q: Please help on all asked questions. Please show all work and steps. Please circle the final answer.…
A: If you have any help please let me know in comment box thankyou.
Q: Instruction: Do not use AI. : Do not just give outline, Give complete solution with visualizations.…
A:
Q: A Give a non-zero vector in the null space of A. -5 35 13 -45 4 -51 -2 4 མག 4 3 -4 -4 -5 Let 18
A:
Q: Solve the system of Linear Equation
A: StepThe given system of linear equations is:x1+2x2−4x3=95x1−x2+2x3=1Step-by-step Solution:This…
Q: Question 5: Show that the nontrivial solution of the equation xy" +y+y=0 Satisfying the conditions…
A: At x=e:
Q: Flux integrals. 1. Let S denote the hemisphere x² + y²+z² = 1, z≥0, which can be written as a…
A:
Q: Q Please solve Advanced mathematics assignment given on page 14 inside this drive, all the required…
A:
Q: Please help on all asked questions. Please show all work and steps. Please circle the final answer.…
A: Let's solve each part step-by-step without calculus. (a) Solve logx​49=−21​ The equation…
Q: A' Reference book: KREYSZIG B[a,b] B(A) BV1a,b BOX, Y) B(A) B(A) Ca C C" C[a, b] C[Q] C(X, Y) (T)…
A:
Q: Suppose a spring with spring constant 2 N/m is horizontal and has one end attached to a wall and the…
A: Introduction:We know the frequency of SHM is given as:f=2π1​mk​​ormk​=(2πf)2orm=(2πf)2k​…
Q: -Q Reported solution Ste ¿Answer question 1 from chapter 6 Please follow this book to answer the…
A:
Q: Find the coordinate vector of v = [6 -4 4] relative to the ordered basis B = ([101], [0 1 1], 1]).…
A: We are given a vector v = [6, -4, 4] and an ordered basis B = ([1, 0, 1], [0, 1, 1], [1, 2, 2]). We…
Q: Problem 6 (Orthogonal Complement). Consider the vector space P2 along with the inner product…
A:
Q: The demand function for a product is modeled by p = 980 - x, 0 ≤ X ≤ 980 where p is the price per…
A: Part (a): Elastic, Inelastic, and Unit Elasticity Elasticity of Demand: Elasticity (E) is given by:…
Q: Instructions to follow: * Give original work *Support your work with examples and graphs where…
A:
Q: How does Batch Normalization improve the training of CNNs? Convolution Neural Network (CNN) Input…
A: Batch Normalization (BN) is a technique that improves the training efficiency and stability of…
Q: Given the differential equation - == y'' + 4y = 3et, y(0) = 0, y'(0) = 0 a) Apply the Laplace…
A: Part (a):Part (b):
Q: Solve this mathematics question 3 from the drive, open link in your browser then ¦request for…
A:
Q: Please help on all asked questions. Please show all work and steps. Please circle the final answer.
A: Define the functions f(x) and g(x) using known pointsf(x): Use (2,0) and (0,2)By intercept…
Q: + ¿Answer question 5 from chapter 6 Please follow this book to answer the question: Ravi P. Agarwal…
A:
Q: This image contains the derivation of the Laplace variational literation method. Help me find the…
A:
Q: Problem 10: Phase Transitions in the Training Dynamics of Neural Networks Statement: Investigate the…
A: Steps to Solve the Problem:
Q: Also, Find the eigenvalues of the​ matrix, set the characteristic polynomial equal to 0 and solve…
A: Step 1:To find the characteristic polynomial and the eigenvalues of the given matrix:A=[−96​−3−6​]…
Q: DO NOT WANT AI SOLUTION.Thank You
A: Step 1: Step 2: Step 3: Step 4:
Q: [1] Find w if (w)s = -3 relative to the basis S = {0 W = 3 -57 6 1 0 } 0
A: Step 1:
Q: Please follow this link and make histogram of the given data. If there is any problem with link…
A: Dataset: Ages of 150 Individuals in a Community[23, 45, 36, 27, 52, 48, 35, 33, 56, 40, 39, 41, 25,…
Q: No Chatgpt please
A:
Q: Find all possible values of a, if any, for which the matrix is not diagonalizable. If there are no…
A: If you have any help please let me know in comment box thankyou.
Q: 3. Find the set of all points on its domain for which f(x, y) = sin x discontinuous. line. +y, x 0.…
A: To determine the set of all points on the domain for which f(x, y) is discontinuous, we analyze the…
Q: please solve the question hand written to understand better
A: Step 1: Step 2: Step 3: Step 4: If the solution was helpful, would you mind marking it as useful on…
Q: Solve advanced math assignment on page 11 in the drive all the required references and lecture…
A:
Q: Statement: Provide a rigorous proof of the Kepler Conjecture, which asserts that the most efficient…
A: Further Research Resources:For deeper insights and rigorous exploration, refer to the following…
Q: On December 6, the nighttime periodwill last twice as long as daylight. If thesun rises at 8:00,…
A: The problem states that the nighttime period is twice as long as the daylight period. We know that a…
Q: (2) For a pair of 20 lb gripping forces, determine the clamping normal force N at each jaw and the…
A:
Q: A small metal bar, whose initial temperature was 20° C, is dropped into a large container of boiling…
A:
Q: Please solve and show all steps.
A: If you have any help please let me know in comment box thankyou.
Q: How many positive integers less than 630 are relatively prime to 630? Use Inclusion-Exclusion…
A: First, we need to find the prime factors of 630. The prime factorization of 630 is 2 * 32 * 5 * 7.
Q: Explain the concept of transfer learning in the context of CNNs. Convolution Neural Network (CNN)…
A: Transfer learning is a powerful machine learning technique that leverages knowledge gained from…
Q: Box answer
A:
Q: A' Reference book: KREYSZIG B[a,b] Introductory Functional Analysis with Applications Complement of…
A:
Q: Please follow this link and make histogram of the given data. If there is any problem with link…
A: Dataset: Daily Temperature Readings (in Celsius) for 100 Days[22, 25, 28, 30, 24, 27, 29, 23, 31,…
Q: 4. (a) (b) (c) 3 The function f is defined by f(x) = x + X Give the domain of f, using appropriate…
A:
Q: Question 4: Real Analysis - Compactness Instructions: Use data from the link provided below and make…
A:
Q: Can I use this method to prove these? Am I right?
A: Steps to Solve the Problem:
Question

Plz don't use chat gpt 

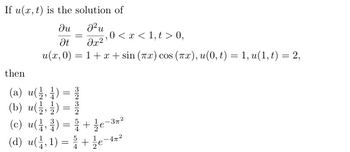
If u(x, t) is the solution of then ди = J²u It მე-2 ა ,0 < x < 1,t > 0, u(x, 0) = 1+x+ sin (πx) cos (πx), u(0, t) = 1, u(1, t) = 2, (a) u() = (b) (ਨੂੰ, ਨੂੰ) = (c) u()+½½-3² = (d) u(1, 1) = e−4 -42
expand button
Transcribed Image Text:If u(x, t) is the solution of then ди = J²u It მე-2 ა ,0 < x < 1,t > 0, u(x, 0) = 1+x+ sin (πx) cos (πx), u(0, t) = 1, u(1, t) = 2, (a) u() = (b) (ਨੂੰ, ਨੂੰ) = (c) u()+½½-3² = (d) u(1, 1) = e−4 -42
expand button
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
See solutionCheck out a sample Q&A here
bartleby

Step by stepSolved in 2 steps

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS