
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
If the
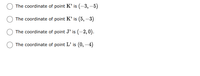
Transcribed Image Text:The options below represent different points and their coordinates on a coordinate plane:
- The coordinate of point K' is \((-3, -5)\).
- The coordinate of point K' is \((5, -3)\).
- The coordinate of point J' is \((-2, 0)\).
- The coordinate of point L' is \((0, -4)\).
Each option is a potential choice represented by a radio button, indicating a typical multiple-choice format. There are no graphs or diagrams to explain.

Transcribed Image Text:**If the triangle below is rotated 90° counterclockwise, which of the following coordinates is correct?**
This graph displays a coordinate plane with a triangle formed by three vertices labeled J, K, and L. The x and y axes intersect at the origin (0,0).
**Vertex Coordinates:**
- Point J is located at (-2, 2).
- Point K is located at (3, 5).
- Point L is located at (4, 0).
To solve the problem, we need to determine the new coordinates of each vertex after a 90° counterclockwise rotation. This transformation involves swapping the coordinates and changing the sign of the new x-coordinate:
For a point (x, y), the new coordinates after a 90° counterclockwise rotation would be (-y, x).
**New Coordinates:**
- Point J (-2, 2) becomes (-2, -2).
- Point K (3, 5) becomes (-5, 3).
- Point L (4, 0) becomes (0, 4).
Thus, the correct new coordinates after the rotation should be calculated and verified as described.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Find an angle between 0 and 360° that is coterminal with the given angle. 394 is coterminal to -140° is coterminal to -2426° is coterminal to 4882° is coterminal toarrow_forwardI need help with Move 4 (the angle is not correct) Thanks in advance!arrow_forwardTriangle QRS has vertices Q(−2, 2) , R(−3, −4) , and S(1, −2) . Write the coordinate notation for a clockwise rotation of 270° about the origin.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning