
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
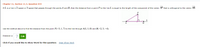
Transcribed Image Text:Chapter 11, Section 11.3, Question 033
If L is a line in 2-space or 3-space that passes through the points A and B, then the distance from
point P to the line L is equal to the length of the component of the vector AP that is orthogonal to the vector AB.
Use the method above to find the distance from the point P(-3, 1,7) to the line through A(1, 1.0) and B(-2,3, -4).
Distance =
Edit
Click if you would like to Show Work for this question: Open Show Work
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Consider (13,3,7) in vector space. Find symmetric equations of a line that contains the point (13,3,7) and the origin. Demonstrate how to check (13,3,7) and (0,0,0) that they fit the equation of the line.arrow_forwardP(2,5, 4) and Q(8,3,3) Let be the line through P in vector direction (1,2,3) and let II be the plane through Q perpendicular to (4,-1,-9). Find an equation for II.arrow_forward16. Determine the vector equation of each line. a) parallel to the y-axis and through Po(-4, 11) b) perpendicular to 5x - 2y = 3 and through Po(7, 1) c) parallel to x + 6y = 1 and through Po(2,-5) d) parallel to the z-axis and through Po(-4, 3, 7) e) parallel to [x, y, z]= [1, 3, -2] + [5, 2, 1] f) the x-intercept of the line is 3 and the y-intercept is -2arrow_forward
- Write the vector equation of the line through (9,-1) and perpendicular to (x,y) = (1,-2) + t(6,-7)arrow_forward4(2). Please show your calculations & explain steps by steps. Determines the vector equation: A) from the line in R2 that goes through the points (3, -6) and (0, -1). B) of the plan in R3 that contains the points (-6, 1, 0), (4, -3, 5) ret (-7, -2, -4).arrow_forwardWhich equations below represent the line in R³ that passes through the point (-3,5,-5) and is parallel to the vector 3i + 4j + 6k? You may select more than one equation. Or(t): +t OF(t) = + t Ox=3+3t; y = 5 + 4t; z = = 5 + 6t - OF(t): = -3, 5, -5> +t OF(t) = +t 1 - x=3+ 6t; y = 5 + 8t; z = 5+ 6t OF(t)= +t OF(t)= + t -arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

