
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
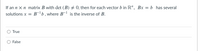
Transcribed Image Text:If an \( n \times n \) matrix \( B \) with \(\det(B) \neq 0\), then for each vector \( b \) in \(\mathbb{R}^n\), \( Bx = b \) has several solutions \( x = B^{-1}b \), where \( B^{-1} \) is the inverse of \( B \).
- True
- False
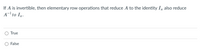
Transcribed Image Text:**Question:**
If \( A \) is invertible, then elementary row operations that reduce \( A \) to the identity \( I_n \) also reduce \( A^{-1} \) to \( I_n \).
- ○ True
- ○ False
**Explanation:**
This question asks whether the same elementary row operations that can transform a matrix \( A \) into the identity matrix \( I_n \) can also transform its inverse \( A^{-1} \) into the identity matrix \( I_n \). Elementary row operations are basic operations used in linear algebra, including row swapping, row multiplication, and row addition, which don't change the solution set of a system.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- what is the x on this matrix; Ax(D+Bx)^-1 = Carrow_forwardCan The solver please include hand written step and all matrix notation possible? Thank you!arrow_forwardShow that if A is square matrix that satisfies the equation 2 A² - A - I = O, then its inverse is A-¹ = 2 A-I. The equation 24² - A - I = O implies that ---Select--- ✓. It follows that ---Select--- ✓. Notice the last equation means that ---Select--- multiplied with A is the identity, which is what we wanted to prove.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

