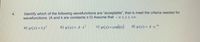
Identify which of the following wavefunctions are "acceptable", that is meet the criteria needed for wavefunctions. (A and k are constants 2 0) Assume that - oo

D(x,0) 0.5 -0.5 -10 -5 5 10 15 20 х (m) D(0,t) 0.5 -0.5 -1 -0.5 0.5 1 1.5 2 2.5 3 t (s) Write down the motion of the wave of the form D(x, t) = A sin(kx – wt+ Po) that %3D matches the above snapshot at time t = 0 and history at location x=0. D(x,t) = m) sin (2 t x/( | m ) -2πt/( s) + (w) a (w) a

Two strings on a musical instrument are tuned to play at 392 Hz (G) and 494 Hz (B). Express your answers using three significant figures. Πν ΑΣφ ? lB Submit Request Answer Part E If their masses and lengths are the same, what must be the ratio of the tensions in the two strings? Express your answers using three significant figures. ? Fr,G FT,B Submit Request Answer II

Equations for the graph y1 = sin⁡(πx − 2πt)   and    y2 = sin((πx/2) + 2πt) Which of the graphs to the left correspond to each of the two initial waves you were given? You may find it helpful to plot these graphs on your own. If you do it by hand, you will gain even more insight. a. The graph that corresponds to y2 is b. The graph that corresponds to the superstition of y1 and y2 is c. The graph that corresponds to y1 is Based on the graph you made for the superposition of y1 and y2, would you consider the superposition to be simple harmonic oscillation? Why or why not. a. Yes. It keeps returning to the equilibrium position. b. No. It is not a simple sine or cosine curve. c. No. Waves and simple harmonic oscillation are two unrelated phenomena. d. Yes. The pattern clearly repeats regularly

Problem 3 Design a FDMA system that carries three message signals: (i) A sinusoidal message of frequency fm1 = 200 Hz, amplitude: 2, (ii) A sinusoidal message of frequency fm2 = 400 Hz, amplitude: 3, and (iii) A sinusoidal message of frequency fm3 = 500 Hz, amplitude: 2. %3D Use carrier signals of frequencies: fc1 = 2000 Hz, fc2 = 5000 Hz and fc3 = 8000 Hz respectively %3D Use AM modulation. (i) (ii) Plot the Composite FDMA signal showing all three AM modulated signals Plot the signal in (i) in frequency domain. Identify the peaks. What do they mean? Now using band pass filters and low pass filters, recover the three messages at the receiver. (i) (ii) Plot the recovered messages in (a) time domain, (b) frequency domain Were you able to recover the original message signal?