
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN: 9781133382119
Author: Swokowski
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Question
Hi i really need help with answering the 4th question in attached image,
thank you so much,
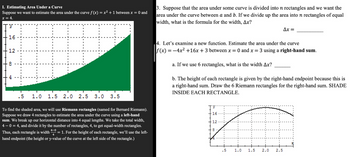
Transcribed Image Text:I. Estimating Area Under a Curve
Suppose we want to estimate the area under the curve f (x) = x² + 1 between x = 0 and
x = 4.
TY
16
12
3. Suppose that the area under some curve is divided into n rectangles and we want the
area under the curve between a and b. If we divide up the area into n rectangles of equal
width, what is the formula for the width, Ax?
Ax =
=
3 using a right-hand sum.
8
LO
4
.5
1.0
1.5 2.0 2.5 3.0
3.5
To find the shaded area, we will use Riemann rectangles (named for Bernard Riemann).
Suppose we draw 4 rectangles to estimate the area under the curve using a left-hand
sum. We break up our horizontal distance into 4 equal lengths. We take the total width,
4 - 0 = 4, and divide it by the number of rectangles, 4, to get equal-width rectangles.
Thus, each rectangle is width = 1. For the height of each rectangle, we'll use the left-
4-0
4
hand endpoint (the height or y-value of the curve at the left side of the rectangle.)
4. Let's examine a new function. Estimate the area under the curve
|f(x) = −4x² +16x + 3 between x = 0 and x
a. If we use 6 rectangles, what is the width Ax?
b. The height of each rectangle is given by the right-hand endpoint because this is
a right-hand sum. Draw the 6 Riemann rectangles for the right-hand sum. SHADE
INSIDE EACH RECTANGLE.
Ty
16
12
.5
1.0 1.5 2.0 2.5
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Find the unknown value. 27. y varies jointly with x and the cube root of 2. If when x=2 and z=27,y=12, find y if x=5 and z=8.arrow_forwardA piece shown by the shaded portion is to be cut from a square plate 128 millimeters on a side. a. Compute the area of the piece to be cut. Round the answer to the nearest square millimeter. b. After cutting the piece, determine the percentage of the plate that will be wasted.arrow_forwardFind length x. All dimensions are in millimetersarrow_forward
- Find the intensity of light at a depth of 12 meter if I0=14 and k=0.7. Round to two decimals.arrow_forwardFind x. All dimensions are in millimeters.arrow_forwardThe carbon content of machine steel for gages usually ranges from 0.15% to 0.25%. Round the answers for a and b to 2 decimal places. a. What is the minimum weight of carbon in 250 kilograms of machine steel? b. What is the maximum weight of carbon in 250 kilograms of machine steel?arrow_forward
- All dimensions are in inches. Round the answers to 3 decimal places. a. If y = 2.8000" find x. b If y = 3.000", find x.arrow_forwardFind the area of a parallelogram bounded by they-axis, the line x=3, the line f(x)=1+2x, and theline parallel to f(x) passing through (2,7).arrow_forwardFind the depth of cut x. All dimensions are in inches.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,  Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage


Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning