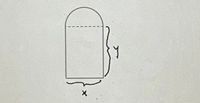
I need help solving this. I only need to write the constraint equation and objective function (don't have to find the minimum cost) using variables x and y. The question states that I'm framing a door that's in the shape of a rectangle with a semicircle on top (no framing along the dotted line). I plan to use 20 ft of framing and the cost of framing for the straight edges is $2/ft and for the circular edge $5/ft. The rectangle has width of "x" and height of "y". Obviously the objective is to minimize cost and the constraint is that there's only 20ft of framing, but I don't know how to use the variables to create a function/equation for the constraint and objective. Especially since there's a semicircle on top, which I know the equation for the perimeter of a semicircle is pi*r+d, but in this case, I think I wouldn't account for "d" because the framing along the dotted line is said to be not part of the question. I'm just not sure how to incorporate the semicircle into the equation.

You are designing a cylindrical barrel that can hold 16π m3 of crude oil. Find the radius r and heighth of the barrel that uses the least amount of material possible.(Hint: The surface area of a cylinder is S = 2πr2 + h(2πr), and its volume is V = πr2h.)(a) Draw a diagram representing this situation.(b) Write the objective and constraint functions.Objective:Constraint:(c) Use the constraint function to write the objective as a function of one variable.(d) Determine the radius and height for the absolute minimum surface area

Please refer to the picture for questions a, b, c, d. Thank you so much.

I need explaination and spreadsheet with formulas and step to step interpretation please.....The attached are first two pages of required assisance and below is  the rest of instructions please consider all of them:c. Suppose the CEO says, “Projects 3 and 4 must be undertaken but not both.”Describe the constraint.d. Suppose the CEO says, “Projects 4 cannot be undertaken unless projects 1 and 3also are both undertaken.” Describe the constraints. Hint: You may need to add more than one constraint for this part.3. [45pts] Multi-product Production Planning. Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows:Department Product 1 Product 2 Product 3A                     1.50           3.00           2.00B                     2.00            1.00         2.50C                     0.25            0.25         0.25During the next production period, the labor-hours…

Determine the amount of slack or surplus for each constraint. If required, round your answers to one decimal place. (1) A + 4B ≤ 21     (2) 2A + B ≥ 7     (3) 3A + 1.5B ≤ 21     (4) -2A + 6B ≥ 0