
Precision Machining Technology (MindTap Course List)
2nd Edition
ISBN: 9781285444543
Author: Peter J. Hoffman, Eric S. Hopewell, Brian Janes
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Please answer and show all work!!!
Transcribed Image Text:hub
blade
R
3R

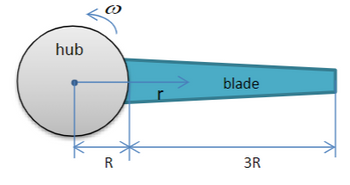
Transcribed Image Text:Problem 1.
An aircraft's propeller consists of a rigid hub of radius R and a flexible tapered
blade of length 3R that has density p (kg/m³). The propeller is rotating about the center of the hub
with a steady angular velocity », thereby creating an effective axial distributed force in the blade.
Neglect forces due to gravity. The cross sectional area distribution of the blade is A(r), defined as
A₁ if R<r< 4R
A(r) = (5) A₁ =
R
(a) Write down the expression for body force due to rotational acceleration.
(b) In the 1D equilibrium equation derived in class, the area of cross section was constant.
Show that the 1D equilibrium equation for the case of a changing cross sectional area is
d(σA)
dr
+ fA = 0.
(c) Write down the boundary conditions for the problem.
(d) Find the axial stress distribution, σ (r).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Recommended textbooks for you
 Precision Machining Technology (MindTap Course Li...Mechanical EngineeringISBN:9781285444543Author:Peter J. Hoffman, Eric S. Hopewell, Brian JanesPublisher:Cengage Learning
Precision Machining Technology (MindTap Course Li...Mechanical EngineeringISBN:9781285444543Author:Peter J. Hoffman, Eric S. Hopewell, Brian JanesPublisher:Cengage Learning Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning
Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning

Precision Machining Technology (MindTap Course Li...
Mechanical Engineering
ISBN:9781285444543
Author:Peter J. Hoffman, Eric S. Hopewell, Brian Janes
Publisher:Cengage Learning

Automotive Technology: A Systems Approach (MindTa...
Mechanical Engineering
ISBN:9781133612315
Author:Jack Erjavec, Rob Thompson
Publisher:Cengage Learning