
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
How do I parameterize the portion from Rei pi/4 to 0?
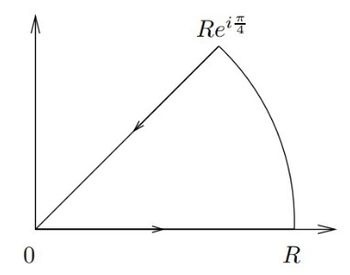
Transcribed Image Text:The image above displays a graph depicting the path of a contour in the complex plane. The contour starts at the origin (0, 0), moves linearly to the point represented by \(Re^{i\frac{\pi}{4}}\), and then follows a curved path back to the point \(R\) on the real axis.
### Graph Explanation:
1. **Axes**:
- The horizontal axis is labeled \(R\) and represents the real part of the complex plane.
- The vertical axis is not labeled but typically represents the imaginary part of the complex plane.
2. **Path Description**:
- The contour begins at the origin, indicated by the point \(0\) at the intersection of the two axes.
- It then proceeds linearly to the point labeled \(Re^{i\frac{\pi}{4}}\). This point is at a distance \(R\) from the origin and makes an angle of \( \frac{\pi}{4}\) (or 45 degrees) with the positive real axis.
- The path then follows a curved line back to the point \(R\) on the real axis. This curved part is an arc, indicating a transition from the angular position \(Re^{i\frac{\pi}{4}}\) to \(R\) along a radial path.
3. **Arrows**:
- The arrows on the graph indicate the direction of the contour. It moves from the origin along a straight line to \(Re^{i\frac{\pi}{4}}\) and then follows an arc back to \(R\).
This graph is typically used in the context of complex analysis to illustrate contour integration, a crucial concept for evaluating integrals over complex functions using paths in the complex plane.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

