3. a. A firm produces two different kinds A and B of a commodity. The daily cost of producing a units of A and y units of B is C(x, y) = 0.04x² +0.01xy +0.01y² + 4x +2y + 500 A sells for $15 per unit and B sells for $9 per unit. Find the daily production levels of x and y that maximize profit per day b.A firm's production function is given by F(K,L) = KL. Each unit of K costs $1.2 and each unit of L costs $0.6. Each unit of output sells at $12. Find the optimal level of K and L that maximize profit.

3. a. A firm produces two different kinds A and B of a commodity. The daily cost of producing a units of A and y units of B is C(x, y) = 0.04x² +0.01xy +0.01y² + 4x +2y + 500 A sells for $15 per unit and B sells for $9 per unit. Find the daily production levels of x and y that maximize profit per day b.A firm's production function is given by F(K,L) = KL. Each unit of K costs $1.2 and each unit of L costs $0.6. Each unit of output sells at $12. Find the optimal level of K and L that maximize profit.

Calculus: Early Transcendentals

8th Edition

ISBN:9781285741550

Author:James Stewart

Publisher:James Stewart

Chapter1: Functions And Models

Section: Chapter Questions

Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...

See similar textbooks

Related questions

Q: 1) An electronic manufacturing firm has the profit function P(x) = - x3 +? x² – ADx + A, and revenue…

A: a. Given, Px=-BAx3+DAx2-ADx+A and Rx=Ax3-Bx2-Dx+AD. The relation between profit, cost and revenue…

Q: The price-demand equations x = f(p, q) and y = g(p, q) represent the num- ber of units demanded of…

A: The weekly price demand equation for A and B. So, the given equation is, (a) It is known that,…

Q: 9. Suppose you sell Dried Chile Mangoes and Biscochitos, each by the pound. Your profit function is…

A: Let x represents the pounds of chile mangoes sold and y represents the pounds of biscochitos sold.…

Q: 2. a.) What comhination of goods rand y should a firm produce to minimize costs when the joint cost…

Q: Q2. You are planning to control pollution from four manufacturing facilities those are discharging…

Q: Output is a function of inputs x1 and x2: y = x₁ 1/4 x2 1/2. Total cost is a function of inputs x₁…

A: Option(2) is true

Q: A firm produces a good from two raw materials X and Y which can be bought at unit prices of pX and…

A: We need to find x and y.

Q: AMBK Company manufactures furniture such as sofas and tables. In their current inven- tory, a total…

A: Each sofa need 4 plank of wood Each table need 2 plank of wood Total availability of wood 48 plank…

Q: 14. A golf ball is chipped out of a sand trap along a path that can be modelled by the quadratic…

A: "Since you have asked multiple questions, we will solve the first question for you. If you want any…

Q: 2. A construction company has to sell at least 60 from one type of equipment(E1) and can be sold…

A: Given that A construction company has two types of equipment. Number of equipment to be sold by the…

Q: MR = 6x2-40x + 50,

Q: The demand function of a monopolist's product is p = √600 – 2q. a. How many units should be produced…

Q: 3. A firm can produce only 1000 units per month. The monthly total cost is given by C(x) = 300 +…

A: To find the maximum profit, we need to maximize the profit function, which is given by the…

Q: 19. The owner of a leather craft shop has determined that he can sell x attaché cases if the price…

A: Profit function is difference of revenue and cost function Derivative of profit is called marginal…

Q: Suppose we are able to model the total utility function for the consumption of two goods, good x and…

A: Given Utility Function : U(x, z) = 3x2 + z2 - 2xz Px = Py = $1 Total Income = $1000

Q: 6. A company produces x units of product A and y units of product B (both in hundreds per month).…

Q: A firm estimates its production function as Q = -2.4 + 20*L -.5*L2 + 30*K -1.00*K2 + 15*F -.3*F2.…

A: Given problem is : A firm estimates its production function as Q = -2.4 + 20*L -.5*L2 + 30*K…

Question

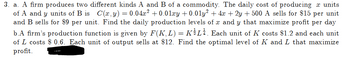
3. a. A firm produces two different kinds A and B of a commodity. The daily cost of producing units
of A and y units of B is C(x, y) = 0.04x² +0.01xy +0.01y² + 4x + 2y + 500 A sells for $15 per unit
and B sells for $9 per unit. Find the daily production levels of x and y that maximize profit per day
b.A firm's production function is given by F(K,L) = KL. Each unit of K costs $1.2 and each unit
of L costs $0.6. Each unit of output sells at $12. Find the optimal level of K and L that maximize
profit.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

SEE SOLUTION Check out a sample Q&A here

Step 1: Step-1

VIEW

Step 2: Step-2

VIEW

Solution

VIEW

Step by step

Solved in 3 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

wouldnt it be -100 not 100 since 7-22=-15

Solution

by Bartleby Expert

SEE SOLUTION

Follow-up Question

how did you get x=100 and y=300 at the end

Solution

by Bartleby Expert

SEE SOLUTION

Similar questions

A manufacturing process has a total cost function given by the equation C = 10 + 4x and a total revenue function given by the equation R = 22x - 4x2 where x is the quantity produced in ’00 units and C and R , are both N$’00. i. Using the cost equation, C = 10 + 4x, identify the value of the company’s fixedcosts (i.e. those that remain constant irrespective of the quantity produced) andvariable costs (i.e. those that vary according to production) for thismanufacturing process. ii. Construct a table to calculate the value of C and R using the values 0, 1, 2, 3, 4and 5 for x. iii. (Using the data from the table in (ii), plot a fully labelled graph for C and Ragainst x. Use the graph drawn in (iii) to determine:iv. The quantity of units produced where the manufacturing process breaks even(i.e. where neither a profit nor a loss is made). v. The range of x in which the manufacturing process makes a profit and the rangein which the manufacturing process makes a loss. vi. The profit or loss…
11. A clothing company sells two types of shoes A and B. The price function for shoe A is (p = 80 5x) dollars. The price function for shoe B is (q = 100 6y) dollars, where (x) and (y) are the numbers of shoe A and shoe B sold per day. The company's cost of producing each shoe A is $20/shoe and the cost of producing each shoe B is $16/shoe. The fixed costs are $200/day. a. Find the Revenue function from selling these two types of shoes. b. Find the Cost function. c. Find the Profit function. d. Perform D-Test. e. Find how many shoes and at the prices at which they should be sold to maximize the daily profit. f. Find the maximum daily profit. 17
Answer all parts. Suppose that a monopolist offers two different products with demand functions P1 = 56 – 4q, Р2 3D 48 — 2q2 The monopolist's joint cost function is C(41, 92) = qỉ + 5q192 + q3 %3D a. Write out the monopolist's profit function as a function of b. Differentiate the profit function with respect to q, and q2.Explain intuitively why we take the derivative of the function. c. Solve the first order conditions using Cramer's rule. d. Use the values that you found in part c to find the prices in each market and the profit that is made by the monopolist. e. Use the second order condition for a maximum to check whether or not the and 92. values that you have computed do represent a maximum.
1. A company sells baseball cards. The cost equation to manufacture the product is given by C (x) = x^2 - x + 31. The company sells its cards for $ 3.00 each. Therefore, your income equation is R (x) = 3x, where R is income and x is the number of units sold in the week (in thousands). Find and interpret the equilibrium point. PLEASE SHOW STEPS CLEARLY.
2. The demand function for a new laptop is p(x) = -3x + 40 where p(x) represents the selling price, in hundreds of dollars, and x is the number of laptops sold, in hundreds. The cost function is C(x) = 16x + 20. a. Determine the profit function. b. Calculate the maximum possible profit.