The first pic is the question. Since some tutors have been solving the problems wrong recently (no judgment), I’ve added a sample question to solve problem. Sample QuestionHockey's Highest Scorers The number of points held by a sample of the NHL's highest scorers for both the Eastern Conference and the Western Conference is shown below. Ata = 0.01, can it be concluded that there is a difference in means based on these data? 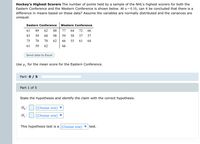Assume the variables are normally distributed and the variances are unequal.Eastern Conference Western Conference77 37 72 5775 78 708862 59 61 9866556164596270 7166687682Send data to ExcelUse u, for the mean score for the Eastern Conference.(a) State the hypotheses and identify the claim with the correct hypothesis.(b) Find the critical value(s).(c) Compute the test value.(d) Make the decision.(e) Summarize the results.Explanation(a) State the hypotheses and identify the claim with the correct hypothesis.The null hypothesis IH, is the statement that there is no difference between the means. This is equivalent to u, -H,.The alternative hypothesis H is the statement that there is a difference between the means. This is equivalent to u, #µ,.The problem asks if "there is a difference in means based on these data." Hence, the claim is the alternative hypothesis H,.(b) Find the critical value(s).For this problem, n, = 13 and n, = 11. The degrees of freedom are the smaller of 13 –1= 12 or 11-1= 10. Hence, d.f. = 10.From OThe t Distribution Table, for a two-tailed test with a = 0.01 and d.f. = 10, the critical values are 13.169.(c) Compute the test value.Use a calculator/computer/formulas in Chapter 3 to compute the sample statistics for each conference. The results are shown below (Round the sample means and standard deviationsto two decimal places):Eastern Conference Western ConferenceSample mean71.9263.55Sample standard deviation12.0611.25Sample size1311Using the formula for the i test-for testing the difference between two means-independent samples, compute the test value:(X, - X2)- (H, – 4-)2.-+-(71.92 – 63.55)-012.06 11.25?1311= 1.757Hence, the test value rounded to three decimal places is t= 1.757.(d) Make the decision.Since the test value does not fall in the critical region, do not reject the null hypothesis. Hockey's Highest Scorers The number of points held by a sample of the NHL's highest scorers for both theEastern Conference and the Western Conference is shown below. At a=0.10, can it be concluded that there is adifference in means based on these data? Assume the variables are normally distributed and the variances areunequal.Eastern ConferenceWestern Conference61896288776472668359609859583757757870626655616461596266Send data to ExcelUse u, for the mean score for the Eastern Conference.Part: 0 / 5Part 1 of 5State the hypotheses and identify the claim with the correct hypothesis.Ho :|(Choose one) ▼H :(Choose one)This hypothesis test is a(Choose one) ▼test.

Answered: Image /qna-images/answer/ea153cb0-1fc8-4ccd-9e0f-1231a70da00d.jpg

Hockey's Highest Scorers The number of points held by a sample of the NHL's highest scorers for both the Eastern Conference and the Western Conference is shown below. At a=0.10, can it be concluded that there is a difference in means based on these data? Assume the variables are normally distributed and the variances are unequal. Eastern Conference Western Conference 61 89 62 88 77 64 72 66 83 59 60 98 59 58 37 57 75 78 70 62 66 55 61 64 61 59 62 66 Send data to Excel Use u, for the mean score for the Eastern Conference. Part: 0 / 5 Part 1 of 5 State the hypotheses and identify the claim with the correct hypothesis. Ho : |(Choose one) ▼ H : (Choose one) ▼ This hypothesis test is a(Choose one) ▼ test.

Hockey's Highest Scorers The number of points held by a sample of the NHL's highest scorers for both the Eastern Conference and the Western Conference is shown below. At a=0.10, can it be concluded that there is a difference in means based on these data? Assume the variables are normally distributed and the variances are unequal. Eastern Conference Western Conference 61 89 62 88 77 64 72 66 83 59 60 98 59 58 37 57 75 78 70 62 66 55 61 64 61 59 62 66 Send data to Excel Use u, for the mean score for the Eastern Conference. Part: 0 / 5 Part 1 of 5 State the hypotheses and identify the claim with the correct hypothesis. Ho : |(Choose one) ▼ H : (Choose one) ▼ This hypothesis test is a(Choose one) ▼ test.

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

Other Math A test consists of two parts. Part 1 consists of 9 questions to be answered true or false. Part 2 consists of 5 multiple-choice questions, each with 4 possible responses. If students are required to complete either Part 1 or Part 2, then find the number of ways to complete this test. The number of ways is
what are some tips to study for the FSA test like the reading and math as well.
In a multiple-choice test, there are three possible answers to each question. There are 10 questions in the exam. One point is given for the correct answer but nothing is deducted for the wrong answer. To pass the exam you must get at least 5 points. Sigmundur is very bad at the study material and therefore decides what the correct answer is in each question. What are the chances that Sigmundur will pass the exam? 1. about 2%. 2. about 7%. 3. about 14%. 4. about 21%.
Solve number 5 and explain
When taking a 12 question multiple choice test, where each question has 3 possible answers, it would be or more questions correct by guessing alone? unusual to get Give your answer in the box above as a whole number.
Thomas scored at the 45th percentile on the midterm. Which interpretation of his score is the best? Group of answer choices 45% of the people tested exceeded his score. Thomas had a better score than 45% of the people tested. Thomas got 45% of the items correct. More than one of the above is appropriate.
What is the purpose of doing a multiple comparison?
For this problem, assume the test had 6 true-false questions and 8 multiple-choice questions, and that each multiple-choice question had 5 choices. How many different answer sheets can be submitted?
Explain about Other Multiple Comparison Tests.
Help!!
When taking a 20 question multiple choice test, where each question has 3 possible answers, it would be unusual to get or more questions correct by guessing alone. Give your answer in the box above as a whole number.
PLEASE HELP SOLVE THE PROBLEM BELOW A candy manufacturer selects mints at random from the production line and weighs them. For one week, the day shift weighed n1 = 194 mints and the night shift weighed n2 = 162 mints. The numbers of these mints that weighed at most 21 grams was y1 = 28 for the day shift and y2 = 11 for the night shift. Let p1 and p2 denote the proportions of mints that weigh at most 21 grams for the day and night shifts, respectively. Give a point estimate of p1 Give the 95% confidence interval for p1 Give a point estimate of p1 − p2 Find the 95% confidence interval for p1 − p2