
Heteroskedasticity arises because of non-constant variance of the error terms. We said proportional heteroskedasticity exists when the error variance takes the following structure: Var(et)=σt^2=σ^2 xt.
But as we know, that is only one of many forms of heteroskedasticity. To get rid of that specific form of heteroskedasticity using Generalized Least Squares, we employed a specific correction – we divided by the square root of our independent variable x. And the reason why that specific correction worked, and yielded a variance of our GLS estimates that was sigma-squared, was because of the following math: (Picture 1)
Where var(et)=σ^2 according to our LS assumptions. In other words, dividing everything by the square root of x made this correction work to give us sigma squared at the end of the expression. But if we have a different form of heteroskedasticity (i.e. a difference variance structure), we have to do a different correction to get rid of it.
(a) what correction would you use if the form of heteroskedasticity you encountered was assumed to be each of the following? Show mathematically (like the equation above does) why the correction you are suggesting would work.
(Picture 2)
(b) using the household income/food expenditure data found the dataset below, use GLS to estimate our model employing the corrections (one model for each correction) you suggested in part (a) above. Fully report your results.
(c) use the Goldfeldt-Quandt test to determine whether your corrections worked from the previous question were successful. Be sure to carry out all parts of the hypothesis tests. Based upon the results of your GQ tests, which of your two corrections do you think works better?
Dataset:
| Food Exp | Wkly Income |
| 52.25 | 258.3 |
| 58.32 | 343.1 |
| 81.79 | 425 |
| 119.9 | 467.5 |
| 125.8 | 482.9 |
| 100.46 | 487.7 |
| 121.51 | 496.5 |
| 100.08 | 519.4 |
| 127.75 | 543.3 |
| 104.94 | 548.7 |
| 107.48 | 564.6 |
| 98.48 | 588.3 |
| 181.21 | 591.3 |
| 122.23 | 607.3 |
| 129.57 | 611.2 |
| 92.84 | 631 |
| 117.92 | 659.6 |
| 82.13 | 664 |
| 182.28 | 704.2 |
| 139.13 | 704.8 |
| 98.14 | 719.8 |
| 123.94 | 720 |
| 126.31 | 722.3 |
| 146.47 | 722.3 |
| 115.98 | 734.4 |
| 207.23 | 742.5 |
| 119.8 | 747.7 |
| 151.33 | 763.3 |
| 169.51 | 810.2 |
| 108.03 | 818.5 |
| 168.9 | 825.6 |
| 227.11 | 833.3 |
| 84.94 | 834 |
| 98.7 | 918.1 |
| 141.06 | 918.1 |
| 215.4 | 929.6 |
| 112.89 | 951.7 |
| 166.25 | 1014 |
| 115.43 | 1141.3 |
| 269.03 | 1154.6 |
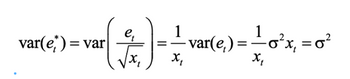

Trending nowThis is a popular solution!
Step by stepSolved in 7 steps with 2 images

- X X zy Section 5.4- QNT/275T: Statistics x + 598163/chapter/5/section/4 for Decision Making home > nce between two population means 4.1: Hypothesis test for the difference between two population means. Jump to level 1 A clinical researcher performs a clinical trial on 14 patients to determine whether a drug treatment has an effect on serum glucose. The sample mean glucose of the patients before and after the treatment are summarized in the following table. The sample standard deviation of the differences was 8. Before treatment What is the test statistic? Ex: 0.123 Check What type of hypothesis test should be performed? Select Select Left-tailed z-test Paired t-test Two-tailed z-test Unpaired t-test Next After treatment 75 Sample mean glucose (mg/dL) What is the number of degrees of freedom? Ex: 25 Does sufficient evidence exist to support the claim that the drug treatment has an effect on serum glucose at the a = 0.05 significance level? Select 81 MESA 81101 2 hp 3 Iarrow_forward9) Find L3.2 (5) using the nodes xo = 3,x1 = 4, x2 = 6 ,x3 = 8 %3Darrow_forwardFind the least square regression line.arrow_forward
- Prove the result that the R^2 associated with a restricted least squares estimator is never larger than that associated with the unrestricted least squares estimator. Conclude that imposing restrictions never improves the fit of the regression.arrow_forwardSuppose we have a multiple regression model with 2 predictors and an intercept. (Without any interaction or higher order terms, we have only the 2 predictors in the model and the intercept.) We have only n= 6 observations (so it would be rather silly to fit this model to this data, but let's pretend it is reasonable). We find the values of the first 5 residuals are: 2.6, 2.3, 2.5, -1.5, -1.4 What is the value of MSRes for this multiple regression model?arrow_forwardAn electrochemical engineer has manufactured a new type of fuel cell (a type of battery)which has to undergo testing to prove its duration: the time it takes to go from fullycharged to completely uncharged, under a fixed nominal load. From the computational simulation models she has, the variance of the duration is σ2 = 4 h2 (hours squared)but she wants to estimate the mean duration time μ. To achieve this she is determinedto do the tests multiple times in independent but identical conditions. Can you findwhat is the smallest number of these tests that she has to do in order for her estimatedmean duration to be within ±0.2 h tolerance of the true mean with 95% certaintyarrow_forward
- The information associated with the maximum likelihood estimator of a parameter 0 is 4n, where n is the number of observations. Calculate the asymptotic variance of the maximum likelihood estimator of 20 . (A) (В) (C) (D) 8n (E) 16narrow_forward5 How does the dynamic CCE estimator solve the estimation problems of the PMG technique?arrow_forwardPlease help with the attached question. Thanksarrow_forward
- when using delta method to calculate variance, shouldn't [g'(μ)]^2 equal to (θ+1)^4?arrow_forwardI need the answer as soon as possiblearrow_forwardLet Y be a random variable with the mgfM(t) = .35e^(−4t) + .1 + .25e^(2t) + .3e^(4t).(a) What is the pmf of Y?(b) Calculate the variance of Y directly from the pmf you determined in part (a).(c) Calculate E[Y^4] directly from the mgf.arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





