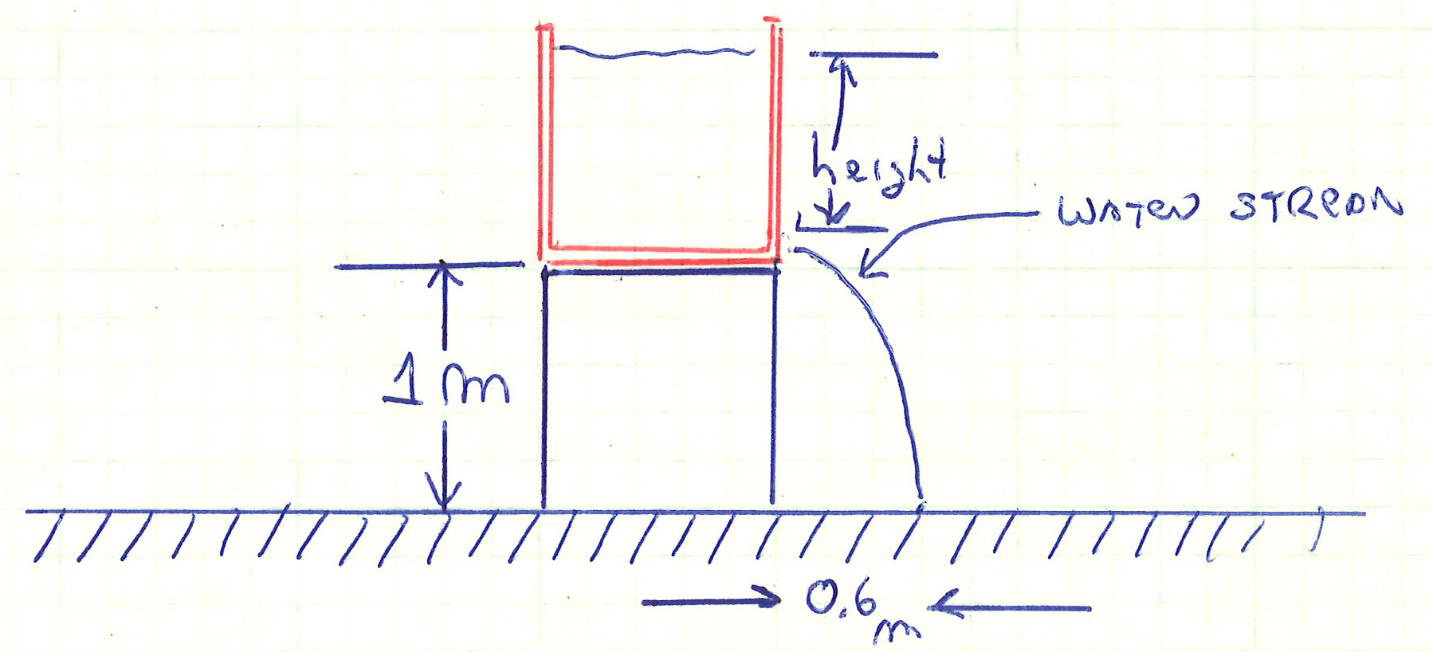
A stream of water shoots out horizontally from a hole in the side of a tank near its bottom. The tank is open to the air. The hole has a radius of rhole = 1.75*10-3 and the tank sits on a 1 m tall platform. The water stream hits the ground a horizontal distance of 0.600 m from the tank. You can assume that the density of the water does not change, that is, the water is incompressible. You can also assume that the flow is steady and nonturbulent.
Equation of Continuity: A2v2 = A1v1
Equation of Hydrostatic Equilibrium: P2 = P1 + pgh (y1 – y2)
Bernoulli’s Equation: P1 + ½pv12 + pgy1 = P2 + ½pv22 + pgy2
a) Using your understanding of parabolic motion, how long (seconds) does it take the water stream to free fall 1 m because of gravity?
b) Again, using your understanding of parabolic motion, what is the horizontal velocity necessary for the stream of water, starting a 1.00 m above the ground, to travel 0.600 m in the time you calculated in part a?
c) If A2 ->> A1 -> A2v2 = A1v1 -> v2 = (A1v1)/A2 = 0. In other words, the area of the surface of the tank is so large compared to the area of the hole that the velocity of fluid at the top of the tank is (by the continuity equation given above) essentially zero. Use the equation of hydrostatic equilibrium (given above) and the result that v2 = 0 to write Bernoulli’s equation in terms of p, g, h, P1, P2, and v1.
d) Assume that the pressure at the top of the tank (P2) is equal to the pressure at the hole (P1) and rewrite Bernoulli’s equation.
e) Solve the equation from part d for the height (a positive number) of the tank?
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images
