
Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
![### Problem 5: Graphing a Trigonometric Function
**Question:**
Graph \( y = 3 - \cos(\pi x) \) over a one-period interval. State its period and the five key points.
**Explanation:**
To graph the function \( y = 3 - \cos(\pi x) \) over a one-period interval, we need to understand the characteristics of the cosine function, including its period, amplitude, phase shift, and vertical shift.
#### Key Characteristics:
1. **Period:** The period of the function \( y = 3 - \cos(\pi x) \) is determined by the coefficient of \( x \) inside the cosine function. For \( \cos(\pi x) \), the period \( T \) is given by:
\[
T = \frac{2\pi}{\pi} = 2
\]
Therefore, the function completes one full cycle over the interval \([0, 2]\).
2. **Amplitude:** The amplitude of the function is 1, as it is the coefficient of the cosine function, but here it is not explicitly visible because the coefficient is implicitly 1. The amplitude indicates the maximum deviation from the midline of the graph.
3. **Vertical Shift:** The function \( y = 3 - \cos(\pi x) \) has a vertical shift of 3 units upwards, meaning the midline of the cosine graph is shifted from \( y=0 \) to \( y=3 \).
4. **Phase Shift:** There is no horizontal shift in this function since there is no horizontal translation term inside the cosine function.
#### Five Key Points:
To plot the graph accurately, we can find the y-values at five key x-values within one period \( [0, 2] \):
- \( x = 0 \)
- \( x = \frac{1}{2} \)
- \( x = 1 \)
- \( x = \frac{3}{2} \)
- \( x = 2 \)
#### Calculations:
1. \( x = 0 \): \( y = 3 - \cos(0) = 3 - 1 = 2 \)
2. \( x = \frac{1}{2} \): \( y = 3 - \cos\left(\pi \cdot \frac{1}{2}\right) = 3](https://content.bartleby.com/qna-images/question/2f9e96de-8215-4532-a7d0-6f1fdf87f241/33fc7dd2-b155-4ddc-88b5-d43de9b1d086/9b6gcgi_thumbnail.png)
Transcribed Image Text:### Problem 5: Graphing a Trigonometric Function
**Question:**
Graph \( y = 3 - \cos(\pi x) \) over a one-period interval. State its period and the five key points.
**Explanation:**
To graph the function \( y = 3 - \cos(\pi x) \) over a one-period interval, we need to understand the characteristics of the cosine function, including its period, amplitude, phase shift, and vertical shift.
#### Key Characteristics:
1. **Period:** The period of the function \( y = 3 - \cos(\pi x) \) is determined by the coefficient of \( x \) inside the cosine function. For \( \cos(\pi x) \), the period \( T \) is given by:
\[
T = \frac{2\pi}{\pi} = 2
\]
Therefore, the function completes one full cycle over the interval \([0, 2]\).
2. **Amplitude:** The amplitude of the function is 1, as it is the coefficient of the cosine function, but here it is not explicitly visible because the coefficient is implicitly 1. The amplitude indicates the maximum deviation from the midline of the graph.
3. **Vertical Shift:** The function \( y = 3 - \cos(\pi x) \) has a vertical shift of 3 units upwards, meaning the midline of the cosine graph is shifted from \( y=0 \) to \( y=3 \).
4. **Phase Shift:** There is no horizontal shift in this function since there is no horizontal translation term inside the cosine function.
#### Five Key Points:
To plot the graph accurately, we can find the y-values at five key x-values within one period \( [0, 2] \):
- \( x = 0 \)
- \( x = \frac{1}{2} \)
- \( x = 1 \)
- \( x = \frac{3}{2} \)
- \( x = 2 \)
#### Calculations:
1. \( x = 0 \): \( y = 3 - \cos(0) = 3 - 1 = 2 \)
2. \( x = \frac{1}{2} \): \( y = 3 - \cos\left(\pi \cdot \frac{1}{2}\right) = 3
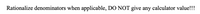
Transcribed Image Text:**Instruction for Mathematical Expressions**
When solving mathematical expressions, it is important to rationalize the denominators whenever applicable. DO NOT provide the value generated by a calculator under any circumstances!
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 5 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON
Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning