What is the graph? Domain & Range? please help?? **Graph the Function Using Transformations**Graph the following function using the techniques of shifting, compressing, stretching, and/or reflecting. Start with the graph of the basic function shown to the right. Find the domain and range of the function.\[ h(x) = \sqrt{x} + 2 \] The image displays a graph of the function $ y = \sqrt{x} $. Below is a detailed explanation:### Description of the Graph:- **Axes**: The graph is plotted on a Cartesian plane with the horizontal axis labeled as $ x $ and the vertical axis labeled as $ y $. Both axes range from $-12$ to $12$.- **Curve**: The function $ y = \sqrt{x} $ is depicted as a curve starting at the origin (0,0) and extending towards the right. The curve is only defined for non-negative values of $ x $ (i.e., $ x \geq 0 $) since the square root of a negative number is not a real number.- **Direction**: The curve rises slowly as it moves to the right, indicating that as $ x $ increases, $ y $ (i.e., $ \sqrt{x} $) also increases, but at a decreasing rate.- **Key Points**: No specific key points are marked on the graph, but it is clear that the curve passes through the origin.### Characteristics of the Function:- **Domain**: $ x \geq 0 $- **Range**: $ y \geq 0 $- **Intercept**: The graph intersects the origin (0,0).This graphical representation is useful for visualizing how the square root function behaves, illustrating its increasing nature and showing its restriction to non-negative values of $ x $.

To graph a function f(x+a), shift the graph of f(x) a units to the left. Therefore, to draw the…

Graph the following function using the techniques of shifting, compressing, stretching, and/or reflecting. Start with the graph of the basic function shown to the right. Find the domain and range of the function.

Graph the following function using the techniques of shifting, compressing, stretching, and/or reflecting. Start with the graph of the basic function shown to the right. Find the domain and range of the function.

Calculus: Early Transcendentals

8th Edition

ISBN:9781285741550

Author:James Stewart

Publisher:James Stewart

Chapter1: Functions And Models

Section: Chapter Questions

Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...

See similar textbooks

Related questions

Q: point-slope form of a line

Q: Explain how to graph the equation x = 2. Can this equation be expressed in slope-intercept form?…

Q: What is the slope of the line that passes through the points (3,3) and (-3,-1). Hint: use graph…

A: Given that the line is passing through the points

Q: please

A: Modern and building more than 10 are red. Good and building from 6 to 10 are blue.

Q: Interpret the meaning of these two slopes.

A: We have given sales(in billions of dollar) of Apple Inc. (plotted in y-axis) in the corresponding…

Q: The line graph to the right shows the total points scored by both teams in a championship game from…

A: Given information: The data represents the line graph of the total points scored by both teams in a…

Q: explain spatial resolution and temporal resolution as they relate to remote sensing data. How would…

A: The ability of a remote sensing sensor to detect details referred to spatial resolution. In spatial…

Q: Select the correct answer. This graph shows the total number of patients seen by a doctor over the…

A: We have to find the domain and range

Q: 2.) y = x² + 2, y = 6 around y = 6.

A: Given that: The curve y = x 2 + 2 , y = 6 around y = 6.

Q: If the graph is a function, write an equation for the graph. You do NOT need to write the…

A: Note:- For given graphs, the axes are not clear. So, equations can be different. You can resubmit…

Q: The points (250,000, 1750) and (100,000, 700) are on the graph of a linear function. The points show…

A: Let two points Slope of the line passing through above two points is given as follows

Q: Please Explain the Graph

A: Given

Q: How do you find the range of coordinate

A: Consider a relation given by set of ordered pairs. x1,y1,x2,y2,x3,y3,..........xn,yn

Q: The amount you eat and your weight is considered positive,negative,zero, or undefined slope

Q: Practice 1. Graph 2x - y ≤ 5. Explain how you know where to shade. -5 0 16

Q: the domain or the range

A: Given Data: Equation: -5t2-15t+t+3=0 For any function y=fx, the domain is x. Here, the function…

Q: Find the slope of the line shown below -3 -2 4 3- 2 -} -2 -3 2 3

Q: Find the slope-intercept form of the equation of the line through the points (-3, 13) and (-1, 5).

A: In algebra, an equation can be defined as a mathematical statement consisting of an equal symbol…

Q: 3. For the graph below, explain how you determine the equation. 3 -2 2 6. -3

Q: Based on grade 11 math student, answer the following question:

A: These graphs demonstrate the difference between linear and quadratic relations visually. The linear…

Q: let's Sweet Tooth... EXTRE Andy wants to eat Chocolate candy and a Chocolate cake for merienda. Andy…

Q: How to bisect a straight line

A: Below are the steps to bisect a line,

Q: State the slope and y-intercept of the graph of 9 – x = 2y.

A: Given, 9-x=2yWe know that, The equation of the line in slope-intercept form is…

Q: Describe how to graph a line using the slope and y-intercept. Provide an original example with your…

A: The equation of a line in slope-intercept form is given by: y=mx+c,Where,m=slope of the…

Question

What is the graph? Domain & Range? please help??

**Graph the Function Using Transformations**

Graph the following function using the techniques of shifting, compressing, stretching, and/or reflecting. Start with the graph of the basic function shown to the right. Find the domain and range of the function.

\[ h(x) = \sqrt{x} + 2 \]

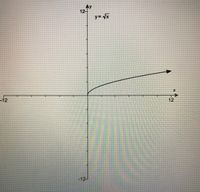
The image displays a graph of the function $ y = \sqrt{x} $. Below is a detailed explanation:

### Description of the Graph:

- **Axes**: The graph is plotted on a Cartesian plane with the horizontal axis labeled as $ x $ and the vertical axis labeled as $ y $. Both axes range from $-12$ to $12$.

- **Curve**: The function $ y = \sqrt{x} $ is depicted as a curve starting at the origin (0,0) and extending towards the right. The curve is only defined for non-negative values of $ x $ (i.e., $ x \geq 0 $) since the square root of a negative number is not a real number.

- **Direction**: The curve rises slowly as it moves to the right, indicating that as $ x $ increases, $ y $ (i.e., $ \sqrt{x} $) also increases, but at a decreasing rate.

- **Key Points**: No specific key points are marked on the graph, but it is clear that the curve passes through the origin.

### Characteristics of the Function:

- **Domain**: $ x \geq 0 $
- **Range**: $ y \geq 0 $
- **Intercept**: The graph intersects the origin (0,0).

This graphical representation is useful for visualizing how the square root function behaves, illustrating its increasing nature and showing its restriction to non-negative values of $ x $.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Inequality$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.

Similar questions

The blue line is a called a line. The red line is called a line.
Explain whether to use x values or y values when describing the domain of a graph. Include a square root graph , it’s domain in interval notation, and explain why.
Name: Date Per Homework: The county fair charges a $10 parking fee. and admission tickets cost $7 per person. Create an equation, table ara graph that describes the relationship between the total cost to attena the fair (©) if Mr. Nguyen purchases'tickets for a certain number of people (p). Equation: Table: Graph: ain.
bottom part about inflection points and graphs not answered
The surface temperature of Neptune is equal to thetemperature of Mercury divided by -1. Find this temperature. Refer the graph below
When the equation is into a fraction how to get rid of the fraction on a graph
can you help graph this please. x > 3 Thank you
A line passes through the points (10,16) and (15, 24). Can the relationship be modeled by a graph of direct variation? Explain in complete sentences how you arrived at your answer. Use complete sentences.