
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN: 9780133923605
Author: Robert L. Boylestad
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
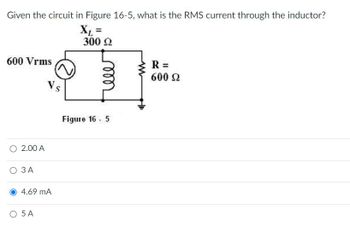
Transcribed Image Text:**Circuit Analysis Problem**
**Question**: Given the circuit in Figure 16-5, what is the RMS current through the inductor?
**Circuit Description**:
- The circuit features an AC voltage source with a voltage of 600 Vrms (root mean square voltage).
- The inductive reactance (\(X_L\)) is 300 Ω.
- A resistor (\(R\)) is in the circuit with a resistance of 600 Ω.
**Diagram Explanation**:
- The diagram depicts a series circuit configuration.
- It includes an AC voltage source labeled \(V_s = 600 \text{ Vrms}\).
- An inductor with inductive reactance \(X_L = 300 \, \Omega\).
- A resistor with \(R = 600 \, \Omega\).
**Answer Options**:
- 2.00 A
- 3 A
- **4.69 mA** (Correct)
- 5 A
**Explanation**:
The problem requires calculating the total impedance of the circuit and then using Ohm’s Law (\(I = \frac{V}{Z}\)) to find the RMS current through the inductor. The impedance in a series RL circuit is calculated using \(Z = \sqrt{R^2 + X_L^2}\). The correct RMS current would then be the result of the division of the Vrms by this total impedance.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A Moving to another question will save this response. Quèstion 2 What is the value of the following complex number in rectangular form? 84 - 20 10 (2+j)(3- 4j) 5+j12/ 0.414+0.628j 0.715+6 56 0 769-112 6 0.75-56 5 dws bAMoving to another question will save this response. =#へarrow_forwardGiven A = 4230° and B = 82–120° Determine the value of the product AB in rectangular form. 32 -j 32 None of the other answers is correct. -0.43 + j 0.25 -28 + j 16 O -1.7 +j 1.0arrow_forwardWhat is the magnitude of the rms value of the current in figure Q 15? 40.0 20.0 0.00 -20.0 40.0 a.0 0.0 15.0 Figure Q15 a. 40 A O b. 88 A O c. 62 A O d. 44 A Leave a messagearrow_forward
- Calculate the impedance and the output voltage of the following circuit.arrow_forwardin a series RL circuit voltage across the resistor is 100 V and the voltage across inductor is 50 v. The power factor of the circuit is O a III Ob 128 D Oc 0.78 O d. 0.89arrow_forward14. Find ZTh a) -j3 Ω b) 0 Ω c)j6Ω d) –9 Ω e) none of these ΕΝΩ tele 170 α ~99 HH P 190 *j15 Ωarrow_forward
- *54. Determine the voltage and its phase angle at each point labeled in Figure 15-103. C3 R1 R3 B D 0.015 µF 1.0 kN 680 0 0.022 µF 1.0 kN V, R6 820 2 1020° V R2 220 2 f = 2.5 kHz C2 0.047 µF R4 910 Narrow_forwardWhat is the a+ib form of: - 2+3i Z = (-2-5i)ei 30°arrow_forwardECTION 16-4 Impedance and Admittance of Parallel RL Circuits 20. What is the impedance in polar form for the circuit in Figure 16-67? 21 What is the impedance in rectangular form for the circuit in Figure 16-67? 22. Repeat Problem 20 for the following frequencies: (a) 1.5 kHz (b) 3 kHz (c) 5 kHz 23. At what frequency does X, equal R in Figure 16-67? ► FIGURE 16-67 15/0° V f=2 kHz (d) 10 kHz m 1₁ L 800 με WI R 12 Ωarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:9781337900348
Author:Stephen L. Herman
Publisher:Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:9780078028229
Author:Charles K Alexander, Matthew Sadiku
Publisher:McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:9780134746968
Author:James W. Nilsson, Susan Riedel
Publisher:PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:9780078028151
Author:Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:Mcgraw-hill Education,