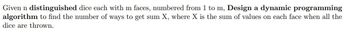
Given n distinguished dice each with m faces, numbered from 1 to m, Design a dynamic programming algorithm to find the number of ways to get sum X, where X is the sum of values on each face when all the dice are thrown.

A linear program is given as follows:   Minimize x1+x2+x3 subject to 2x1 – 6x2 + 3x3 ≥ 50 3x1 + 4x2 -x3 ≥ 40 4x1 – x2 + 5x3 ≥ 60 x1, x2 ≥ 0   Solve the problem using a linear programming solver (e.g., linprog in python). What is the optimum solution? What are the values of x1, x2 and x3 for this optimum solution?   Instructions: Submit the following The new form of the problem (if you have changed the form) for linear programming solver input Code to solve the problem Answers of questions ‘a’ and ‘b’

consider a jewler who shows a collection of diamonds to a person. all diamonds have different integer ounce weights and are laid out in a single row on the table. what is the largest weight amount of diamonds that the person can take, provided that the person cannot select adjacent diamonds?  use standard pseudocode notation similar to python to write a dynamic programming bottom up algorithm that solves this problem for any n number of diamonds.

X-Kingdom has trapped n number of soldiers of their opponent. They want to execute them. They created a strategy so that the prisoners will kill each other and at the end one prisoner will be alive and eventually released. As part of the process, they assigned each trapped soldier a sequence number starting from 1 and ending at n.    If n = 5 and k = 2, then the safe position is 3. Firstly, the person at position 2 is killed, then person at position 4 is killed, then person at position 1 is killed. Finally, the person at position 5 is killed. So, the person at position 3 survives. If n = 7 and k = 3, then the safe position is 4. The people at positions 3, 6, 2, 7, 5, 1 are killed in order, and the person at position 4 survives.   Input:n and k Output:Print the list of prisoners in reverse order from n to 1Then reverse the list to print it in correct order from 1 to nDisplay the position number who will survive. You must have to use circular doubly linked list for your solution. You…