**GIVEN MESSAGE IS CAB2; IT IS NOT AB12** This homework relates to hash functions for block ciphers (sec 11.3.2)  Block size = 8 bits  Hash size = 8 bits  Encryption function: Divide the key into two halves: LK and RK; Divide the plaintext into two halves: LT and RT; Then ciphertext= LC||RC where LC=LK XOR RT; and RC = RK XOR LT; where LC, RC, LT, and RT are each 4 bits; Plaintext and ciphertext are each 8 bits. 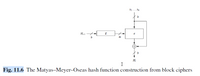 g(H) = an 8-bit string that is equal to the complement of bits in H; For example, if H=A3 (Hexa) = 10100011 (binary); then g(H)= 01011100  H0 = Initial hash = 11001010 Given a message m: CAB2 (in Hexa); Q.3 Determine the hash (in hexadecimal) of the message M using Migayuchi-Preneel hash function (Fig. 11.6)

Exercise 2 (MAC schemes derived from block ciphers( Let E denote the family of encryption functions for a block cipher where plaintext blocks, ciphertext blocks, and keys are each n = 80 bits in length. Let H {0, 1} {0, 1}" be a hash function. Assume that plaintext messages m all have bit-lengths that are multiples of n; we write m = (my, m₂,...,m), i.e. m is composed of t blocks m, of n bits each. Consider the following MAC schemes, each using an n-bit secret key k. 1. MAC (m) = ₁, where co = 0, and c, =c-1m, Ex(m) for 1 ≤ i ≤t. 2. MAC (m) Ek(H(m)). Are any of these MAC schemes secure? Justify your answer and clearly state any assumptions you make.

Question # 1: Use the Multiplicative Cipher method to encrypt the following plaintext:We will succeed in our ventureKey length K = 7 You must show all the steps of your workQuestion # 2: Use the additive cipher with key = 15 to decrypt the message “WTAAD”.You must show all the steps of your work Question # 3: Use the concept of a one-way hash function to encrypt the following name into a 9 x 9 -dimensional database table. Jonathan Leea) How many rows and columns are there on this tableb) Which indices is Jonathan on this tablec) Why are hash functions relevant in database encryption?d) What would you do to remedy the problem of index congestion on your database?You must show all the steps of your work Question # 4: Use the multiplicative method to decrypt the following ciphertext.MADWU Key = 5You must show all the steps of your workQuestion # 5: use the XOR technique to encrypt the following statement before transmission: The quick brown fox jumps over the lazy dog

3. Consider an example of hash table of size 30, and the following items are to be stored. Design the hash table and the final array in the obtained indexes. (14, 22) (11, 18) (52,71) (41, 20) (30, 29) (33,64)

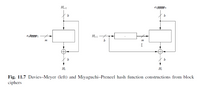
#include <stdio.h>#include <stdlib.h>#include <string.h>#define capacity 101 // Size of Hash Table int hash_function(char* str) {    int i = 0;    for (int j=0; str[j]; j++)        i += str[j];    return i % capacity;} struct Ht_item {    char* name;    int numberCourses;}; // Hash Table Definitionstruct HashTable {    struct Ht_item** items;    int size;    int count;}; struct Ht_item* create_item(char* key, int value) {        struct Ht_item* item = (struct Ht_item*) malloc (sizeof(struct Ht_item));    item->name = (char*) malloc (strlen(key) + 1);    item->numberCourses = value;     strcpy(item->name, key);    item->numberCourses = value;     return item;} struct HashTable* create_table(int size) {    // Creates a New Hash Table    struct HashTable* table = (struct HashTable*) malloc (sizeof(struct HashTable));    table->size = size;    table->count = 0;    table->items = (struct Ht_item**) calloc (table->size, sizeof(struct Ht_item*));…

import hashlib def hash_function(password, salt, al):  if al == 'md5':    #md5    hash = hashlib.md5(salt.encode() + password.encode())    hash.update(password.encode('utf-8'))    return hash.hexdigest() + ':' + salt  elif (al == 'sha1'):    #sha1      hash = hashlib.sha1()    hash.update(password.encode('utf-8'))    return hash.hexdigest() + ':' + salt  elif al == 'sha224':    #sha224    hash = hashlib.sha224()    hash.update(password.encode('utf-8'))    return hash.hexdigest() + ':' + salt  elif al == 'sha256':    #sha256    hash = hashlib.sha256()    hash.update(password.encode('utf-8'))    return hash.hexdigest() + ':' + salt  elif al == 'blake2b':    #blake2b512    hash = hashlib.blake2b()    hash.update(password.encode('utf-8'))    return hash.hexdigest() + ':' + salt  else:    print("Error: No Algorithm!") if __name__ == "__main__":  # TODO: create a list called hash_list that contains  # the five hashing algorithsm as strings  # md5, sha1, sha224, sha256, blake2b    hash_list =…

**GIVEN MESSAGE IS CAB2; IT IS NOT AB12**This homework relates to hash functions for block ciphers (sec 11.3.2) Block size = 8 bits Hash size = 8 bits Encryption function: Divide the key into two halves: LK and RK; Divide the plaintext into twohalves: LT and RT; Then ciphertext= LC||RC where LC=LK XOR RT; and RC = RK XOR LT;where LC, RC, LT, and RT are each 4 bits; Plaintext and ciphertext are each 8 bits. g(H) = an 8-bit string that is equal to the complement of bits in H; For example, if H=A3 (Hexa)= 10100011 (binary); then g(H)= 01011100 H0 = Initial hash = 11001010Given a message m: CAB2 (in Hexa);Q1. Determine the hash (in hexadecimal) of the message M using Martyas-Meyer-Oseas hashfunction (Fig. 11.7).Q2. Determine the hash (in hexadecimal) of the message M using Davis-Meyer hash function(Fig. 11.6)Q3. Determine the hash (in hexadecimal) of the message M using Migayuchi-Preneel hashfunction (Fig. 11.6) **GIVEN MESSAGE IS CAB2; IT IS NOT AB12**

Please solve this

PYTHON Why am I getting an error and it doesn't show the right output?  Problem 1# Implement a hashtable using an array. Your implementation should include public methods for insertion, deletion, and# search, as well as helper methods for resizing. The hash table is resized when the loadfactor becomes greater than 0.6# during insertion of a new item. You will be using linear probing technique for collision resolution. Assume the key to# be an integer and use the hash function h(k) = k mod m where m is the size of the hashtable. class HashTableProb:    def __init__(self, size=10):        # Initialize the hashtable with the given size and an empty array to hold the key-value pairs.        self.__size = size # size of the hashtable        self.__hashtable = [None for _ in range(size)]        self.__itemcount = 0 # Keeps track of the number of items in the current hashtable     def __contains__(self, key):        return self.__searchkey(key)     def __next_prime(self, x):        def…

write code for :