
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
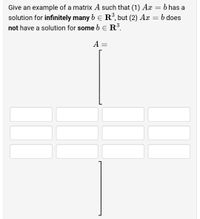
Transcribed Image Text:b has a
Give an example of a matrix A such that (1) Ax
solution for infinitely many b E R°, but (2) Ax = b does
not have a solution for some b e R.
A =
Expert Solution
arrow_forward
Step 1
If the dimension of the column space of A will be 3 (or if A has set of three linearly independent column.) then A span and we have infinitely many b.
And if the dimension of the column space of A will be less than 3 than A does not span and we get no solution for some b.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- -1 1 -3 2 2 -3 -2] M³+c₁M² + c₂M + c3I3 = 0, where I3 is the identity 3 x 3 matrix. Let M C1 || C2 = C3 = -3] 3. Find C₁, C₂, and c3 such that 1arrow_forwardLet M = -5 M2 + c, M + c2I, = 0, where I, is the identity 2 x 2 matrix. 3 Find c and c2 such that C1 = C2arrow_forwardGiven the matrix A = 0 2 2 0 2 2 find an orthogonal diagonalization of A: A = QDQ" Enter each matrix Q and D in the format [[a11 , a12 , a13] , [a21 , a22 , a23] , [a31, a32, a33]]. Note: if you need to enter a square root of a number x you can do it as follows: sqrt (x). Alternatively, you can compute matrix entries in the decimal form rounded to 3 decimal places, and enter them in this. Matrix Q: Matrix D:arrow_forward
- Consider the matrix A = 0 Is this matrix positive definite? Is this matrix positive semidefinite? Justify your answer.arrow_forwardlet A be an mxn matrix and v and w vectors in Rn. If v and w were both solutions to Ax=0, show that v+w is also a solution to Ax=0.arrow_forwardIf 3AT = 3 -6 2). then the a1,2 entry of the matrix A isarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

