Question
Please help with this question:
Determine the running time of the following algorithms. Write summations to represent loops and simplify. Show all work. If bounding is used, the upper and lower bounds must only differ by a constant. Note: This is not the line-by-line analysis method. Loops are inclusive.
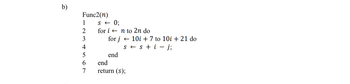
Transcribed Image Text:b)
Func2(n)
1
2
3
4
5
6
7
S← 0;
for in to 2n do
for j
end
10i + 7 to 10i + 21 do
ss + i- j;
end
return (s);
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- Please help me with this question. I am not understanding what to do. Please complete part 2 for the question. I am extremely confused (You do not need to do the contents of ex 5 Just need the part 2 for the question)arrow_forwardRecursion efficiency in Julia can be improved using memorization technique to store the values of previously computed functions. The following Fibonacci function below does not employ memorization, please change into a recursive function with memorization: function fib(n) if n==1 return 1 elseif n==2 return 1 elseif n<=0 printstyled("Invalid input",color=:red) return else return fib(n-1)+fib(n-2) end endarrow_forwardExpress the linear search algorithm as a recursive procedurearrow_forward
arrow_back_ios
arrow_forward_ios