MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Topic Video
Question
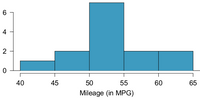
5.8 Fuel efficiency of Prius: Fueleconomy.gov, the official US government source for fuel economy information, allows users to share gas mileage information on their vehicles. The histogram below shows the distribution of gas mileage in miles per gallon (MPG) from 14 users who drive a 2012 Toyota Prius. The sample
(a) The EPA claims that a 2012 Prius gets 50 MPG (city and highway mileage combined). Do these data provide strong evidence against this estimate for drivers who participate on fueleconomy.gov?
The hypotheses for the test are:
- Ho: μ = 50
Ha: μ < 50 - Ho: μ = 50
Ha: μ ≠ 50 - Ho: μ = 50
Ha: μ > 50
To execute this hypothesis test we should use a:
- Z-test
- T-Test
because:
- σ is known, but the
sample size is less than 30 - σ is known and the population is normal
- σ is unknown and the sample size is less than 30
There are ______ degrees of freedom for this test.
The test statistic is: _______________ (please round to two decimal places)
The p-value for this hypothesis test is: __________ (please round to four decimal places)
The conclusion for the hypothesis test is:
- Since p<α we reject the null hypothesis and accept the alternative
- Since p ≥ α we accept the null hypothesis
- Since p ≥ α we reject the null hypothesis and accept the alternative
- Since p ≥ α we do not have enough evidence to reject the null hypothesis
- Since p<α we fail to reject the null hypothesis
(c) Calculate a 95% confidence interval for the average gas mileage of a 2012 Prius by drivers who participate on fueleconomy.gov.
We are __________ % confident that the true population gas mileage of a 2012 Prius by drivers who participate on fueleconomy.gov is between ______ mpg and _______ mpg. (please round to one decimal place)
Transcribed Image Text:### Understanding Mileage Distribution Through a Histogram
#### Graph Explanation:
The graph displayed above is a histogram illustrating the distribution of mileage (measured in miles per gallon, MPG) for a sample of vehicles.
**Key Features of the Graph:**
- **X-axis (Horizontal Axis):** Represents the mileage of vehicles, expressed in miles per gallon (MPG). The values range from 40 MPG to 65 MPG.
- **Y-axis (Vertical Axis):** Indicates the frequency of vehicles within each mileage range. The values on this axis range from 0 to 6.
**Data Representation:**
- The histogram comprises multiple bars, each representing a specific range of mileage.
- The height of each bar corresponds to the number of vehicles that fall within that particular mileage range.
**Detailed Breakdown of the Histogram:**
- The first bar (40 to 45 MPG) shows that approximately 1 vehicle falls within this mileage range.
- The second bar (45 to 50 MPG) indicates that around 2 vehicles have mileages in this range.
- The most prominent bar (50 to 55 MPG) is the tallest, indicating that 6 vehicles fall within this mileage range, making it the most common mileage category in the dataset.
- The bars representing the ranges 55 to 60 MPG and 60 to 65 MPG both indicate that about 2 vehicles fall within these ranges each.
**Conclusion:**
The histogram clearly demonstrates that the majority of vehicles in this dataset have mileages between 50 and 55 MPG, while fewer vehicles fall into the lower or higher mileage ranges. This type of histogram is a valuable tool for visually summarizing and understanding the distribution of vehicle efficiencies in a given sample.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- A study reported on essential organic molecules and a Normal model can be used to describe these levels in adults. If the mean is 194 mg/dL and a standard deviation is 28, complete the following questions. a) Draw and label the Normal model. b) What percent of adults do you expect to have this essential organic molecule, cholesterol, levels over 210 mg/dL? c) What percent of adults do you expect to have cholesterol levels between 150 and 170 mg/dL? d) Estimate the interquartile range of cholesterol levels. IQR=___________mg/dL e) Above what value are the highest 15% of adults' cholesterol levels? ___________mg/dLarrow_forwardIdentify the mean, median and mode based from the data below.arrow_forwardIn your work as a biomedical engineer, you need to better understand the distribution of adults' blood pressures. Specifically, you are interested in systolic blood pressure, which is a measure of pressure within arteries when a heart beats; this is the first number in a blood pressure reading. In healthy adults, systolic blood pressure has a normal distribution with a mean of 112 mm Hg and standard deviation of 10 mmHg. Before you collect sample data, you want to predict the range in which you expect almost all of the data to fall. Which of the following represents the interval that will likely contain almost all (~99.7%) of the sample measurements of healthy adult systolic blood pressure? A) (102 mm Hg, 122 mm Hg) B) (92 mm Hg, 132 mm Hg) C) (82 mm Hg, 142 mm Hg) D) (72 mm Hg, 152 mm Hg)arrow_forward
- A study by the National Center for Health Statistics suggested that women between the ages 20 and 29 in the US have a mean BMI of 26.8 with a standard deviation of 7.4. A BMI of 30 or greater is considered as being obese. What proportion of women in this age range are obese?arrow_forwardFind the mode, mean, and standard deviation of the following data: 3, 2, 3, 4, 6arrow_forwardAccording to the U.S. Census, the average adult woman is the United States is 65 inches tall and the standard deviation is 3 inches. If Zsike is 67 inches tall, what is her z-score?arrow_forward
- Choose the correct option and explain.arrow_forwardplease answer asaparrow_forwardThe U.S. Center for Disease Control reports that in year 1900, the mean life expectancy is 47.6 years for whites and 33 years for nonwhites. (Click here for reference data) Suppose a survey of randomly selected death records for white and nonwhite people born in 1900 from a certain county is conducted. Of the 110 whites surveyed, the mean life span was 48.2 years with a standard deviation of 11.2 years and of the 95 nonwhites, the mean life span was 39.3 years with a standard deviation of 16 years. Conduct a hypothesis test at the 0.05 level of significance to determine whether there was no difference in mean life spans in the county for whites and nonwhites in year 1900. Preliminary: Is it safe to assume thatnw≤5% of all white people born in 1900 andnnw≤5% of all nonwhite people born in 1900? No Yes Is nw≥30 and nnw≥30 ? No Yes Test the claim: Determine the null and alternative hypotheses. H0: μw μnw Ha: μw μnw Determine the test statistic. Round to four…arrow_forward
- what measure of variability is to be computed with a medianarrow_forwardAs reported in Runner's World magazine, the times of the finishers in the New York City 10- km run are normally distributed with mean 61 minutes and standard deviation 9 minutes. The 75th percentile for the finishing times is 67 minutes. What is the interpretation of this value?arrow_forwardFuel efficiency of Prius: Fueleconomy.gov, the official US government source for fuel economy information, allows users to share gas mileage information on their vehicles. The histogram below shows the distribution of gas mileage in miles per gallon (MPG) from 14 users who drive a 2012 Toyota Prius. The sample mean is 53.3 MPG and the standard deviation is 5.2 MPG. Note that these data are user estimates and since the source data cannot be verified, the accuracy of these estimates are not guaranteed. (a) The EPA claims that a 2012 Prius gets 50 MPG (city and highway mileage combined). Do these data provide strong evidence against this estimate for drivers who participate on fueleconomy.gov? The test statistic is: __________________(please round to two decimal places)The p-value:___________________________ for this hypothesis test is: (please round to four decimal places)(c) Please comment on the primary thing that is wrong about the following statement: There is sufficient evidence…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman