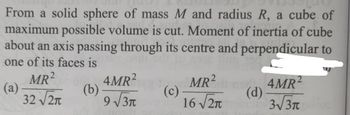
From a solid sphere of mass M and radius R, a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is MR² (b) 32 √2n (a) 4MR² 9√√3π (c) MR² 16 √2T (4MR² 3√√3π (d)

Your answer is partially correct. Review Conceptual Example 2 before attempting this problem. The moon has a diameter of 3.48 x 106 m and is a distance of 3.85 x 108 m from the earth. The sun has a diameter of 1.39 x 10⁹ m and is 1.50 x 10¹1 m from the earth. Determine (in radians) the angles subtended by (a) the moon and (b) the sun, as measured by a person standing on the earth. (c) Determine the ratio of the apparent circular area of the moon to the apparent circular area of the sun. These calculations determine whether a total eclipse of the sun is really "total." (a) Number 0.00904 (b) Number i 0.0093 (c) Number i 0.945 Units rad Units Units rad No units

A uniform solid disk of mass m = 2.99 kg and radius r = 0.200 m rotates about a fixed axis perpendicular to its face with angular frequency 6.05 rad/s. (a) Calculate the magnitude of the angular momentum of the disk when the axis of rotation passes through its center of mass. kg • m2/s (b) What is the magnitude of the angular momentum when the axis of rotation passes through a point midway between the center and the rim? kg • m2/s

A uniform solid disk of mass m = 2.99 kg and radius r = 0.200 m rotates about a fixed axis perpendicular to its face with angular frequency 5.99 rad/s. (a) Calculate the magnitude of the angular momentum of the disk when the axis of rotation passes through its center of mass. |kg · m2/s (b) What is the magnitude of the angular momentum when the axis of rotation passes through a point midway between the center and the rim? |kg · m2/s

A force vector, F = 3i− 12j, acts at a distance vector of r = 0.2i m from the axis of rotation on a wheel. It has a moment of inertia of 3 kgm^2.  If we assume the full mangitude of the torque causes rotation, what is the angular acceleration caused by the force?

In the figure, two particles, each with mass m = 0.88 kg, are fastened to each other, and to a rotation axis at 0, by two thin rods, each with length d = 5.6 cm and mass M = 1.3 kg. The combination rotates around the rotation axis with angular speed w = 0.28 rad/s. Measured about O, what is the combination's (a) rotational inertia and (b) kinetic energy? M. M. Rotation axis (a) Number i Units (b) Number i Units